Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=4x\Rightarrow y=2x^2+1-4x\)
\(y'\left(x\right)=4x-4=0\Rightarrow x=1\)

1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm

Chọn B.
Ta có:  ; f(0) = a + 2.
; f(0) = a + 2.
Vậy để hàm số liên tục tại x = 0 thì a + 2 = 1 ⇔ a = -1.

\(f'\left(x\right)=x^2-4\sqrt{2}x+8=\left(x-2\sqrt{2}\right)^2\)
\(f'\left(x\right)=0\Rightarrow\left(x-2\sqrt{2}\right)^2=0\Rightarrow x=2\sqrt{2}\)

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
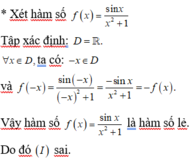
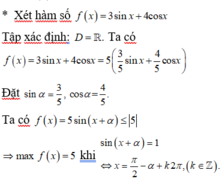

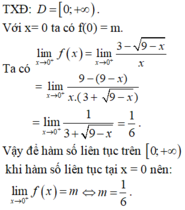
Đề là \(f\left(x\right)=\dfrac{1}{2}sin2x-cosx-x+2015\) đúng không nhỉ?
\(f'\left(x\right)=cos2x+sinx-1\)
\(f'\left(x\right)=0\Leftrightarrow cos2x+sinx-1=0\)
\(\Leftrightarrow1-2sin^2x+sinx-1=0\)
\(\Leftrightarrow sinx\left(1-2sinx\right)=0\Rightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)