Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có:
f x = ∫ f ' x d x = ∫ d x x 2 − 1 = 1 2 ∫ 1 x − 1 − 1 x + 1 d x = 1 2 ln x − 1 x + 1 + C
Với
− 1 < x < 1 ⇒ f x = 1 2 ln 1 − x x + 1 + C 1
Với
x > 1 x < − 1 ⇒ f x = 1 2 ln x − 1 x + 1 + C 2
Do f − 3 + f 3 = 0 và
f − 1 2 + f 1 2 = 2 ⇒ 1 2 ln 2 + C 2 + 1 2 ln 1 2 + C 2 = 0 1 2 ln 3 + C 1 + 1 2 ln 1 3 + C 1 = 2 ⇔ C 2 = 0 C 1 = 1
Do đó
P = f 0 + f 4 = 1 + 1 2 ln 3 5

Đáp án C.
Đặt z = a + b i , a , b ∈ ℝ . Ta có 1 − i z 2 + 2 + 2 i z 2 + 2 z z + i = 0 .
Với a 2 + b 2 > 0 ⇒ z ≠ 0 ; z 2 = z . z ¯ . Ta có
1 ⇔ 1 − i . z . z ¯ + 2 + 2 i z 2 + 2 z z + i = 0 ⇔ 1 − i z ¯ + 2 + 2 i z + 2 z + i = 0
⇔ 1 − i a − b i + 2 + 2 i a + b i + 2 a + b + 1 i = 0
⇔ a − b − a + b i + 2 a − 2 b + 2 a + 2 b i + 2 a + 2 b + 2 i = 0
⇔ 5 a − 3 b + a + 3 b + i = 0 ⇔ 5 a − 3 b = 0 a + 3 b = − 2 ⇔ a = − 1 3 b = − 5 9 ⇒ F = 3 5
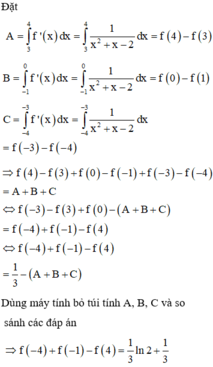
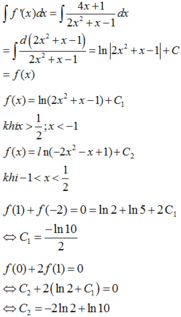
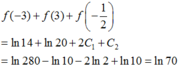

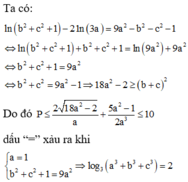
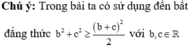
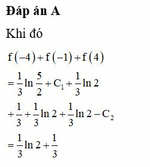

Đáp án C.
Ta có ∫ f ' x d x = ln 2 x − 1 + C
Nếu x > 1 2 ⇒ f x = ln 2 x − 1 + C
mà f 1 = 2 ⇒ C = 2
Vậy f x = ln 2 x − 1 + 2 khi x > 1 2
Tương tự f x = ln 1 − 2 x + 1 k h i x < 1 2
Do đó f − 1 + f 3 = ln 3 + 1 + ln 5 + 2 = ln 15 + 3.