Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
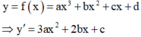
Nhìn vào đồ thị của hàm số y = f '(x) ta nhận thấy đồ thị hàm số đi qua các điểm (1;0), (3;0), (2;1) nên có hệ phương trình sau:
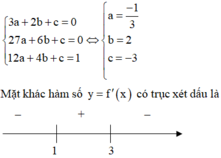
Nên đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3
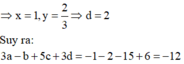

Đáp án A
Xét hệ phương trình
f ' ( x ) = 3 x 2 + 6 a x + 3 = 0 ( * ) g ' ( x ) = 3 x 2 + 6 b x + 9 = 0 ⇒ 6 x ( a − b ) = 6 ⇔ x = 1 a − b .
Áp dụng công thức nghiệm do phương trình (*) ta có x = − a ± a 2 − 1 với a ∈ ( − ∞ ; − 1 ) ∪ 1 ; + ∞ .
*Trường hợp 1: x = − a + a 2 − 1 .
Ta có
1 a − b = − a + a 2 − 1 ⇔ b = a + 1 a − a 2 − 1 = 2 a + a 2 − 1
Suy ra
P = a + 2 b = a + 4 a + 2 a 2 − 1 ≥ 5 a + 2 a 2 − 1
Xét hàm số
f ( x ) = 5 x + 2 x 2 − 1 ; x ∈ − ∞ ; − 1 ∪ 1 ; + ∞ .
Đạo hàm
f ' x = 5 + 2 x x 2 − 1 ; f ' x = 0 ⇔ 5 x 2 − 1 = − 2 x ⇔ x ≤ 0 25 x 2 − 1 = 4 x 2
⇔ x = − 5 21 (thỏa mãn).
Lại có f − 5 21 = − 21 ⇒ P ≥ 21 (lập bảng biến thiên của hàm số f x ).
*Trường hợp 2:Tương tự, ta tìm được P ≥ 21 .

Đáp án A
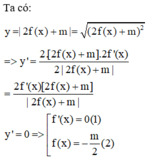
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy