Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
9.
\(f\left(x\right)=F'\left(x\right)=3ax^2+2bx+c\)
\(\left\{{}\begin{matrix}f\left(1\right)=2\\f\left(2\right)=3\\f\left(3\right)=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a.1+2b.1+c=2\\3a.2^2+2b.2+c=3\\3a.3^2+2b.3+c=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a+2b+c=2\\12a+4b+c=3\\27a+6b+c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0\\b=\frac{1}{2}\\c=1\end{matrix}\right.\)
\(\Rightarrow F\left(x\right)=\frac{1}{2}x^2+x+1\)
10.
\(F\left(x\right)=\int\frac{x-2}{x^3}dx=\int\left(\frac{1}{x^2}-\frac{2}{x^3}\right)dx=\int\left(x^{-2}-2x^{-3}\right)dx\)
\(=-1.x^{-1}+x^{-2}+C=-\frac{1}{x}+\frac{1}{x^2}+C\)
\(F\left(-1\right)=3\Leftrightarrow1+1+C=3\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\frac{1}{x}+\frac{1}{x^2}+1\)
4.
\(\int\left(x^3-\frac{3}{x^2}+2^x\right)dx=\frac{1}{4}x^4-\frac{3}{x}+\frac{2^x}{ln2}+C\)
5.
\(\int e^{2019x}dx=\frac{1}{2019}\int e^{2019x}d\left(2019x\right)=\frac{1}{2019}e^{2019x}+C\)
6.
\(\int sin2018x.dx=\frac{1}{2018}\int sin2018x.d\left(2018x\right)=-\frac{1}{2018}cos2018x+C\)
7.
\(\int\frac{x^2-x+1}{x-1}dx=\int\left(\frac{x\left(x-1\right)}{x-1}+\frac{1}{x-1}\right)dx=\int\left(x+\frac{1}{x-1}\right)dx=\frac{1}{2}x^2+ln\left|x-1\right|+C\)
8.
\(F\left(x\right)=\int\left(2x+1\right)^3dx=\frac{1}{2}\int\left(2x+1\right)^3d\left(2x+1\right)=\frac{1}{8}\left(2x+1\right)^4+C\)
\(F\left(\frac{1}{2}\right)=4\Leftrightarrow\frac{1}{8}\left(2.\frac{1}{2}+1\right)^4+C=4\Rightarrow C=2\)
\(\Rightarrow F\left(x\right)=\frac{1}{8}\left(2x+1\right)^4+2\Rightarrow F\left(\frac{3}{2}\right)=\frac{1}{8}4^4+2=34\)
Câu 1:
\(\int\limits^3_0\left(f'\left(x\right)+1\right)\sqrt{x+1}dx=\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx+\int\limits^3_0\sqrt{x+1}dx\)
\(=\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx+\frac{14}{3}=\frac{302}{15}\Rightarrow\int\limits^1_0f'\left(x\right)\sqrt{x+1}dx=\frac{232}{15}\)
Ta có:
\(I=\int\limits^3_0\frac{f\left(x\right)dx}{\sqrt{x+1}}\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=\frac{dx}{\sqrt{x+1}}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=2\sqrt{x+1}\end{matrix}\right.\)
\(\Rightarrow I=2f\left(x\right)\sqrt{x+1}|^3_0-2\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx\)
\(=4f\left(3\right)-2f\left(0\right)-2.\frac{232}{15}\)
\(=2\left(2f\left(3\right)-f\left(0\right)\right)-\frac{464}{15}=36-\frac{464}{15}=\frac{76}{15}\)
Câu 2:
\(I_1=\int\limits^3_1\frac{xf'\left(x\right)}{x+1}dx=0\)
Đặt \(\left\{{}\begin{matrix}u=\frac{x}{x+1}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{\left(x+1\right)^2}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I_1=\frac{xf\left(x\right)}{x+1}|^3_1-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}=\frac{3.3}{3+1}-\frac{1.3}{1+1}-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=\frac{3}{4}-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=0\)
\(\Rightarrow\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=\frac{3}{4}\)
Ta có:
\(I=\int\limits^3_1\frac{f\left(x\right)+lnx}{\left(x+1\right)^2}dx=\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx+\int\limits^3_1\frac{lnx}{\left(x+1\right)^2}dx=\frac{3}{4}+I_2\)
Xét \(I_2=\int\limits^3_1\frac{lnx}{\left(x+1\right)^2}dx\Rightarrow\) đặt \(\left\{{}\begin{matrix}u=lnx\\dv=\frac{1}{\left(x+1\right)^2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{dx}{x}\\v=\frac{-1}{x+1}\end{matrix}\right.\)
\(\Rightarrow I_2=\frac{-lnx}{x+1}|^3_1+\int\limits^3_1\frac{dx}{x\left(x+1\right)}=-\frac{1}{4}ln3+\int\limits^1_0\left(\frac{1}{x}-\frac{1}{x+1}\right)dx\)
\(=-\frac{1}{4}ln3+ln\left(\frac{x}{x+1}\right)|^3_1=-\frac{1}{4}ln3+ln\frac{3}{4}-ln\frac{1}{2}=\frac{3}{4}ln3-ln2\)
\(\Rightarrow I=\frac{3}{4}+\frac{3}{4}ln3-ln2\)
Chọn B
Để g( x) = f( x+ 1) => g’(x) = f’( x+1)
Hàm số y= g’(x) = f’( x+ 1) có đồ thị là phép tịnh tiến của đồ thị hàm số y= f’(x) theo phương trục hoành sang trái 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x)= f’( x+1) vẫn cắt trục hoành tại 1 điểm.
Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).
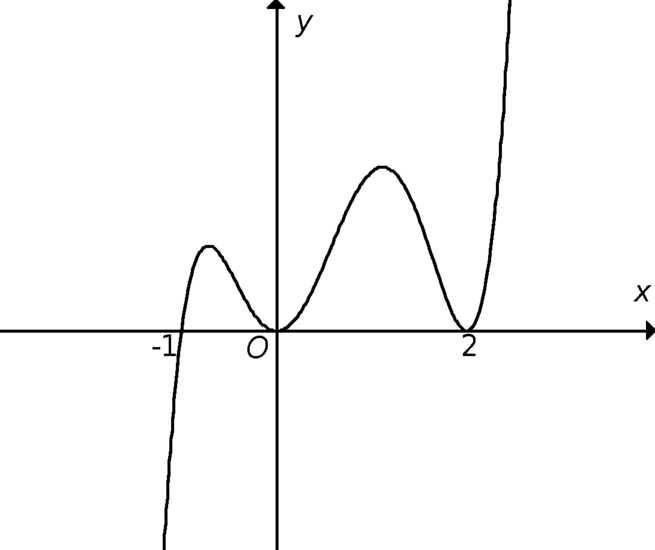
Dựa vào đồ thị ta thấy phương trình 
chỉ có một nghiệm đơn và hai nghiệm kép nên 
chỉ đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số f(x) có đúng một cực trị.
Chọn A.
Bài 1:
\(F'\left(x\right)=e^x+\left(x-1\right)e^x=xe^x=\frac{x}{e^x}.e^{2x}\Rightarrow f\left(x\right)=\frac{x}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\v=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}+2\int f\left(x\right).e^{2x}dx=x.e^x+2\left(x-1\right)e^x+C=\left(3x-2\right)e^x+C\)
2.
Xét \(J=\int\limits^1_0xf\left(6x\right)dx\)
Đặt \(6x=t\Rightarrow dx=\frac{1}{6}dt\Rightarrow J=\frac{1}{36}\int\limits^6_0t.f\left(t\right)dt=\frac{1}{36}\int\limits^6_0x.f\left(x\right)dx=1\)
\(\Rightarrow I=\int\limits^6_0x.f\left(x\right)dx=36\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\frac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow I=\frac{1}{2}x^2f\left(x\right)|^6_0-\frac{1}{2}\int\limits^6_0x^2.f'\left(x\right)dx\)
\(\Leftrightarrow36=18-\frac{1}{2}\int\limits^6_0x^2f'\left(x\right)dx\)
\(\Rightarrow\int\limits^6_0x^2f'\left(x\right)dx=-36\)
.
.
.
.
\(x\left(x+1\right)f'\left(x\right)+f\left(x\right)=x^2+x\)
\(\Leftrightarrow\frac{x}{x+1}.f'\left(x\right)+\frac{1}{\left(x+1\right)^2}f\left(x\right)=\frac{x^2+x}{\left(x+1\right)^2}=\frac{x}{x+1}\)
\(\Leftrightarrow\left(\frac{x}{x+1}.f\left(x\right)\right)'=\frac{x}{x+1}=1-\frac{1}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\frac{x}{x+1}f\left(x\right)=\int\left(1-\frac{1}{x+1}\right)dx=x-ln\left|x+1\right|+C\)
Thay \(x=1\) vào ta được
\(\frac{1}{1+1}f\left(1\right)=1-ln2+C\Rightarrow C=\frac{f\left(1\right)}{2}+ln2-1=-1\)
\(\Rightarrow\frac{x}{x+1}f\left(x\right)=x-ln\left|x+1\right|-1\)
Thay \(x=2\) vào ta được:
\(\frac{2}{3}f\left(2\right)=2-ln3-1\Rightarrow f\left(2\right)=\frac{3}{2}\left(1-ln3\right)=\frac{3}{2}-\frac{3}{2}ln3\)
\(\Rightarrow a^2+b^2=\left(\frac{3}{2}\right)^2+\left(-\frac{3}{2}\right)^2=\frac{9}{2}\)
Phương pháp để dẫn tới cách giải trên như sau:
Nhìn vế trái, ta thấy nó có dạng gần giống với biểu thức đạo hàm của một tích, vậy ta cố gắng đưa vế trái thành đạo hàm của một tích.
Giả sử sau khi biến đổi, ta được vế trái có dạng: \(VT=\left(u.f\right)'\) ta cần tìm hàm \(u\left(x\right)\) này
\(\Rightarrow VT=u.f'+u'.f\)
Chia cho \(u\) ta được: \(\frac{VT}{u}=f'+\frac{u'}{u}.f\)
Chỉ cần quan tâm tới dạng \(f'+\frac{u'}{u}.f\) (1)
Nói chung là ta cần triệt tiêu toàn bộ hệ số đằng trước \(f'\left(x\right)\)
Ta biến đổi biểu thức ban đầu về dạng (1) bằng cách chia biểu thức điều kiện cho \(x\left(x+1\right)\)
\(f'\left(x\right)+\frac{1}{x\left(x+1\right)}f\left(x\right)=\frac{x^2+x}{x\left(x+1\right)}\) (2)
Chỉ quan tâm tới vế trái của (2), đồng nhất nó với (1) ta thấy:
\(\frac{u'}{u}=\frac{1}{x\left(x+1\right)}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{u'}{u}dx=\int\frac{1}{x\left(x+1\right)}dx\Leftrightarrow ln\left(u\right)=ln\left(\frac{x}{x+1}\right)\Rightarrow u=\frac{x}{x+1}\)
Vậy ta đã biết hàm \(u\left(x\right)\) cần tìm là \(u\left(x\right)=\frac{x}{x+1}\)
Chọn D
Với
ta có:
Vì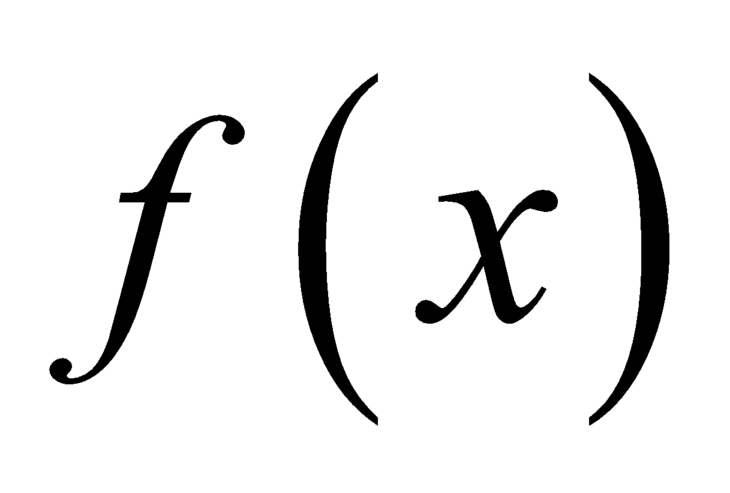
liên tục tại 
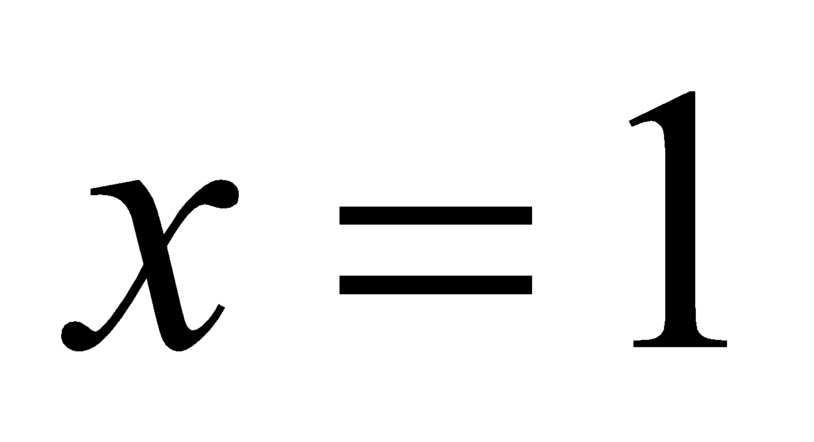nên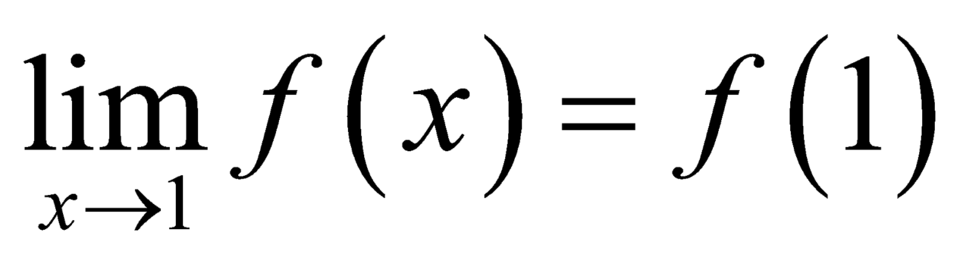 
hữu hạn.
Do đó: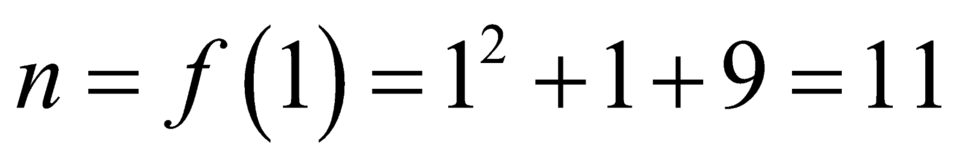
.
Vậy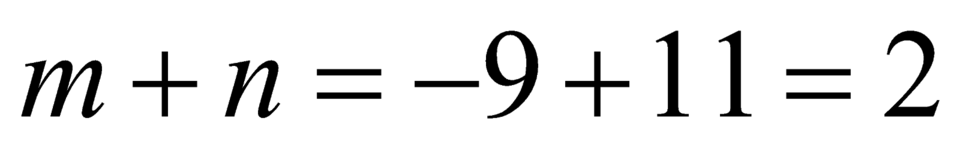
.