Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số gia của hàm \(f\left(x\right)\) phải ứng với số gia \(\Delta x\) của đối số chứ sao lại \(\Delta t\), em kiểm tra lại đề bài

Tập xác định của hàm số đã cho là D= [2/3;+∞)
Với ∆x là số gia của đối số tại x=2 sao cho 2+∆x ∈ D,thì
Δ y = 3 ( Δ x + 2 ) − 2 − 3.2 − 2 = 3 Δ x + 4 − 2
Chọn đáp án C

1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

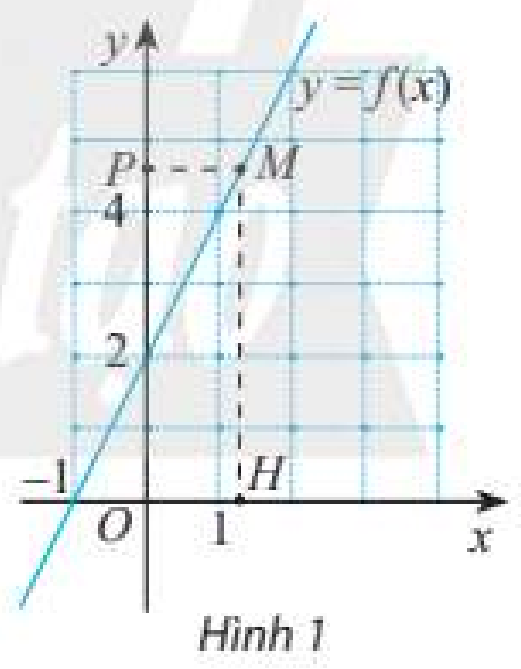
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).

1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)
2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)
3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)
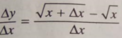
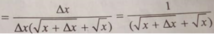
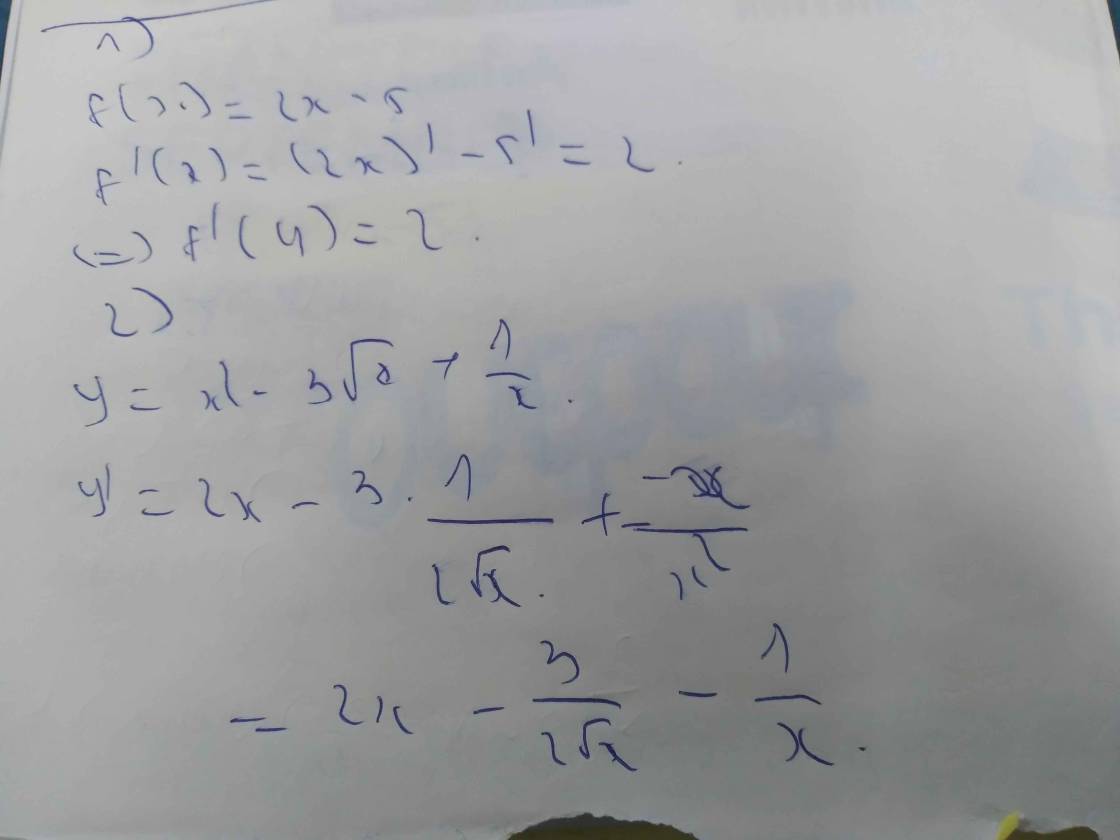


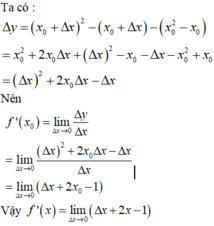
∆y=f(1+∆x)-f(1)=(1+∆x)2+2(1+∆x)-(1+2)=(∆x)2+4∆x
Đáp án B
Chú ý. Tránh các sai lầm thay trực tiếp ∆x hoặc 1 vào hàm (A,D) hoặc lấy hiệu của f(∆x) và f(1) (C)