Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì
\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\)
\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)
Từ đó ta dễ dàng tổng quát được:
\(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)
Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)
Áp dụng công thức trên ta được:
\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)
Bạn tự rút gọn kết quả nhé
\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

\(f\left(x\right)=\dfrac{x^2-1+1}{1-x}=-\left(x+1\right)-\dfrac{1}{x-1}\)
Sau 2 lần đạo hàm thì \(-\left(x+1\right)\) sẽ về 0 nên ta có:
\(f^{\left(n\right)}\left(x\right)=\dfrac{\left(-1\right)^{n+1}.n!}{\left(x-1\right)^{n+1}}\) với \(n\ge3\)

Chọn A
Cách 1: Từ đồ thị hàm số của ![]() ta thấy
ta thấy ![]() có hai cực trị dương nên hàm số
có hai cực trị dương nên hàm số ![]() lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số
lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số ![]() với trục tung nữa ta được tổng cộng là
với trục tung nữa ta được tổng cộng là ![]() cực trị.
cực trị.

Chọn đáp án D
![]()
![]()
![]()
![]()
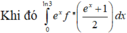
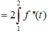

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy