Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
ta có
f ( x ) = 2 m x - m x 3 ⇒ f ' ( x ) = 2 m - 3 m x 2
Vì x= 1 là nghiệm của bất phương trình f ' ( x ) ≤ 1 nên
2 m − 3 m .1 2 ≤ 1 ⇔ − m ≤ 1 ⇔ m ≥ − 1

- Ta có: f ' ( x ) = m - x 2 .
- Do x = -1 là nghiệm của bất phương trình f'(x) < 2.
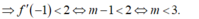
Chọn B.

Ta có f ' x = m − x 2 .
Để x= - 1 là nghiệm của bất phương trình
f ' ( x ) < 2
⇒ f ' 1 < 2 ⇔ m − 1 < 2 ⇔ m < 3.
Chọn đáp án B

\(f'\left(x\right)=2m-3mx^2\)
\(f'\left(x\right)\le1\Rightarrow2m-3mx^2\le1\Leftrightarrow3mx^2\ge2m-1\)
- Với \(x=1\Rightarrow3m\ge2m-1\Rightarrow m\ge-1\)

1.
\(f'\left(x\right)=3x^2-6mx+3\left(2m-1\right)\)
\(f'\left(x\right)-6x=3x^2-3.2\left(m+1\right)x+3\left(2m-1\right)>0\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+2m-1>0\)
\(\Leftrightarrow x^2-2x-1>2m\left(x-1\right)\)
Do \(x>2\Rightarrow x-1>0\) nên BPT tương đương:
\(\dfrac{x^2-2x-1}{x-1}>2m\Leftrightarrow\dfrac{\left(x-1\right)^2-2}{x-1}>2m\)
Đặt \(t=x-1>1\Rightarrow\dfrac{t^2-2}{t}>2m\Leftrightarrow f\left(t\right)=t-\dfrac{2}{t}>2m\)
Xét hàm \(f\left(t\right)\) với \(t>1\) : \(f'\left(t\right)=1+\dfrac{2}{t^2}>0\) ; \(\forall t\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t\right)>f\left(1\right)=-1\Rightarrow\) BPT đúng với mọi \(t>1\) khi \(2m< -1\Rightarrow m< -\dfrac{1}{2}\)
2.
Thay \(x=0\) vào giả thiết:
\(f^3\left(2\right)-2f^2\left(2\right)=0\Leftrightarrow f^2\left(2\right)\left[f\left(2\right)-2\right]=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế giả thiết:
\(-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\) (1)
Thế \(x=0\) vào (1) ta được:
\(-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
\(\Leftrightarrow f^2\left(2\right).f'\left(2\right)+4f\left(2\right).f'\left(2\right)-12=0\) (2)
Với \(f\left(2\right)=0\) thế vào (2) \(\Rightarrow-12=0\) ko thỏa mãn (loại)
\(\Rightarrow f\left(2\right)=2\)
Thế vào (2):
\(4f'\left(2\right)+8f'\left(2\right)-12=0\Leftrightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1\)

Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)
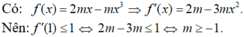
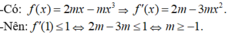
Chọn B