Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 2 nên
( d ) đi qua A( 2,0 )
Thay A( 2,0 ) vào đường thẳng d ta được
\(\left(1-m\right).2+m+2=0\)
\(2-2m+m+2=0\)
\(4-m=0\)
\(m=4\)
b, Đường thẳng d song song vs đường thẳng y = 2x - 1 nên
1 - m = 0 và m + 2 khác -1
m = 1 và m khác -3

a, Hoành độ giao điểm (P) ; (d) thỏa mãn pt
\(x^2=2x-m\Leftrightarrow x^2-2x+m=0\)
Để pt có 2 nghiệm pb khi \(\Delta'=1-m>0\Leftrightarrow m< 1\)
Vậy với m < 1 thì (P) cắt (d) tại 2 điểm pb
b, Theo Vi et \(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=m\end{cases}}\)
Ta có : \(\frac{1}{x_1^2}+\frac{1}{x_2^2}=2\Leftrightarrow\frac{x_1^2+x_2^2}{x_1^2x_2^2}=2\)
\(\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=2\)Thay vào ta có :
\(\Leftrightarrow\frac{4-2m}{m^2}=2\Leftrightarrow4-2m=2m^2\Leftrightarrow2m^2+2m-4=0\)
mà a + b + c = 0 => 2 + 2 - 4 = 0
vậy pt có 2 nghiệm
\(m_1=1\left(ktm\right);m_2=-2\left(tm\right)\)

a) Khi \(m=1\) \(\Rightarrow\left(d\right):y=2x+8\)
Xét phương trình hoành độ giao điểm
\(x^2=2x+8\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
+) Với \(x=4\Rightarrow y=16\)
+) Với \(x=-2\Rightarrow y=4\)
Vậy khi \(m=1\) thì (P) cắt (d) tại 2 điểm phân biệt \(\left(4;16\right)\) và \(\left(-2;4\right)\)
b) Xét phương trình hoành độ giao điểm
\(x^2-2x+m^2-9=0\) (*)
Ta có: \(\Delta'=10-m^2\)
Để (P) cắt (d) \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta'=10-m^2>0\) \(\Leftrightarrow-\sqrt{10}< m< \sqrt{10}\)
Theo đề: (P) cắt (d) tại 2 điểm nằm về 2 phía của trục tung
\(\Leftrightarrow\) Phương trình (*) có 2 nghiệm trái dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1x_2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}10-m^2>0\\m^2-9< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{10}< m< \sqrt{10}\\-3< m< 3\end{matrix}\right.\) \(\Leftrightarrow-3< m< 3\)
Vậy ...

a) Khi m = 2 thì: \(\hept{\begin{cases}y=x^2\\y=2x+3\end{cases}}\)
Hoành độ giao điểm (P) và (d) là nghiệm của PT: \(x^2=2x+3\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\Rightarrow y=1\\x=3\Rightarrow y=9\end{cases}}\)
Vậy tọa độ giao điểm của (P) và (d) là \(\left(-1;1\right)\) và \(\left(3;9\right)\)
b) Hoành độ giao điểm của (P) và (d) là nghiệm của PT:
\(x^2=mx+3\Leftrightarrow x^2-mx-3=0\)
Vì \(ac=1\cdot\left(-3\right)< 0\) => PT luôn có 2 nghiệm phân biệt
Theo hệ thức viet ta có: \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-3\end{cases}}\)
Mà \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=\frac{3}{2}\Leftrightarrow\frac{-m}{3}=\frac{3}{2}\Rightarrow m=-\frac{9}{2}\)
Vậy \(m=-\frac{9}{2}\)

Gọi \(M\left(x;-\frac{2}{3}x+\frac{5}{3}\right)\) thuộc (d).
Ta có \(O\left(0;0\right)\). Vậy \(OM^2=x^2+\left(\frac{5}{3}-\frac{2}{3}x\right)^2=\frac{13}{9}x^2-\frac{20}{9}x+\frac{25}{9}=\frac{13}{9}\left(x-\frac{10}{13}\right)^2+\frac{25}{13}\ge\frac{25}{13}\)
Suy ra \(OM\ge\frac{5}{\sqrt{13}}\). Đẳng thức xảy ra khi \(x=\frac{10}{13}\)
Vậy \(M\left(\frac{10}{13};\frac{15}{13}\right)\) thì khoảng cách OM ngắn nhất.

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

1: Khi m=3/2 thì \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x+3=2x+3\)
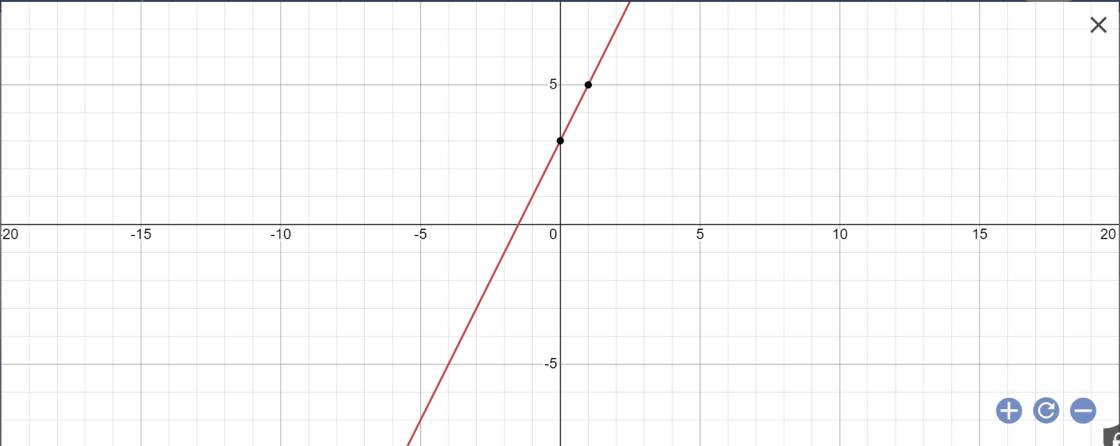
2: \(tanx=a=2m-1\)
3:
Để hai đồ thị (d) và (d') song song với nhau thì:
\(2m-1=3\)
=>2m=4
=>m=2
4: Thay x=1 vào (d1), ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(2m-1\right)+3=-1\)
=>2m+2=-1
=>2m=-3
=>\(m=-\dfrac{3}{2}\)
5: y=1
=>2x-3=1
=>2x=4
=>x=2
Thay x=2 và y=1 vào (d),ta được:
\(2\left(2m-1\right)+3=1\)
=>2(2m-1)=-2
=>2m-1=-1
=>2m=0
=>m=0