Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
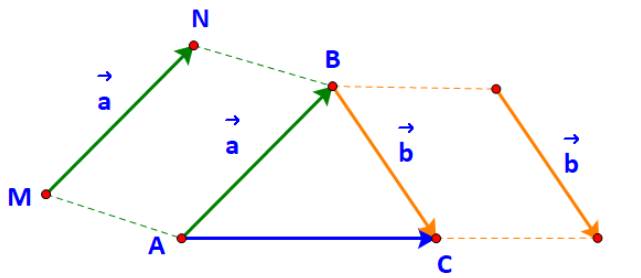
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

\(\overrightarrow{x}\) ⊥ \(\overrightarrow{y}\)
⇒ \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{2a}-\overrightarrow{b}\right)=0\). Đặt \(\left|\overrightarrow{a}\right|=a;\left|\overrightarrow{b}\right|=b\)
⇒ 2a2 - \(\overrightarrow{a}.\overrightarrow{b}\) + 2\(\overrightarrow{a}.\overrightarrow{b}\) - b2 = 0
⇒ \(\overrightarrow{a}.\overrightarrow{b}\) = b2 - 2a2 = 4 - 4 = 0
⇒ \(\left(\overrightarrow{a};\overrightarrow{b}\right)=90^0\)

a) Ta có \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\overrightarrow{MA}+\overrightarrow{BC}\) = \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MG}\)
⇒\(\left|\overrightarrow{MG}\right|=\left|\overrightarrow{BA}\right|\)
⇒ M là điểm trên đường tròn tâm G bk là AB

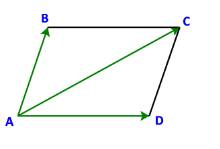
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.

\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=4\)
⇒ \(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=16\)
⇒ 16 + 9 - 2\(\overrightarrow{a}.\overrightarrow{b}\) = 16
⇒ \(2\overrightarrow{a}.\overrightarrow{b}=9\)
⇒ cosα = \(\dfrac{9}{2.4.3}\)
⇒ cos α = \(\dfrac{3}{8}\)
Vậy chọn D
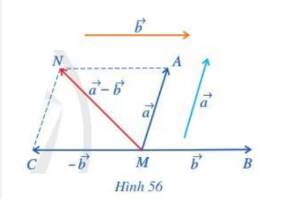

a) Đặt D, E lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Ta có: \(\overrightarrow {MA} = \overrightarrow a \)hay \(\overrightarrow {MA} = \overrightarrow {DE} \)
\( \Leftrightarrow MAED\) là hình bình hành.
Do đó A là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \)và điểm M.
Tương tự ta có:
B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \)và điểm M.
Lại có: \(\overrightarrow {MC} = - \overrightarrow b = - \overrightarrow {MB} \) do đó \(MC = MB\) và hai vecto \(\overrightarrow {MB} ,\overrightarrow {MC} \) ngược hướng nhau.
Hay M là trung điểm đoạn thẳng BC.
b) Lấy N là đỉnh thứ tư của hình bình hành AMCN.
Khi đó ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \)
Mà: \(\overrightarrow {MA} = \overrightarrow a ;\;\overrightarrow {MC} = - \overrightarrow b \)
\( \Rightarrow \overrightarrow a + ( - \overrightarrow b ) = \overrightarrow {MN} \).