Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A\subset B\Leftrightarrow\left\{{}\begin{matrix}m>5\\m+2< 6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>5\\m< 4\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
\(B\subset A\Leftrightarrow\left\{{}\begin{matrix}5>m\\6< m+2\end{matrix}\right.\) \(\Leftrightarrow4< m< 5\)
\(B\ne\varnothing\Rightarrow A\cap B\ne\varnothing\) với mọi m \(\Rightarrow\) ko tồn tại m để A hợp B = rỗng (câu này là giao mới đúng)

\(A\cap B=\varnothing\)\(\Leftrightarrow\left[{}\begin{matrix}m\ge3\\m+1< 0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\ge3\\m< -1\end{matrix}\right.\)
Ta có nên làm bánh mì sữa không, ngồi trong phòng mọc nấm mất... Nhưng mà hong có men, haizz, lười quá

\(A=\left[m;m+1\right]\)
\(B=\left[0;3\right]\)
\(A\cap B=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1< 0\\m>3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\) thỏa mãn đề bài

Điều kiện để A xác định là:
\(m-1< 8\)
\(\Leftrightarrow m< 8+1\Leftrightarrow m< 9\)
Để: \(A\backslash B=\varnothing\)
\(\Leftrightarrow A\subset B\) \(\Rightarrow2\le m-1\)
\(\Leftrightarrow m\ge3\)
kết hợp với điều kiện:
\(\Rightarrow3\le m< 9\)

Bàu này quá dễ cái này lớp 6 còn còn có trong chương trình :)
Cho hai tập khác rỗng : A = (m – 1; 4], B = (-2; 2m + 2), với m ∈ Rℝ. Giá trị m để A ∩ B ⊂ (-1; 3) là:
Điều kiện để tồn tại tập hợp A, B là
{m−1<4−2<2m+2⇔{m<5m>−2⇔−2<m<5A∩B⊂(−1;3)⇔{m−1≥−12m+2≤3⇔{m≥0m≤12⇔0≤m≤12m-1<4-2<2m+2⇔m<5m>-2⇔-2<m<5A∩B⊂(-1;3)⇔m-1≥-12m+2≤3⇔m≥0m≤12⇔0≤m≤12
Kết hợp với điều kiện (*) ta có 0 ≤ m ≤ 1/2 là giá trị cần tìm.
Cách này là tôi tự làm trong 1 lần ở Viet Jack kiểu tham khảo chứ ko coppy mạng :)
>3.....@Chi
Điều kiện để tồn tại tập hợp A, B là
\(\hept{\begin{cases}m-1>4\\-2< 2m+2\end{cases}}\Rightarrow\hept{\begin{cases}m< 5\\m>-2\end{cases}}\Leftrightarrow-2< m< 5\)
A ∩ B ⊂ (-1; 3) \(\Leftrightarrow\hept{\begin{cases}m-1\ge-1\\2m+2\le3\end{cases}}\Leftrightarrow\hept{\begin{cases}m\ge0\\m\le\frac{1}{2}\end{cases}}\Leftrightarrow0\le m\le\frac{1}{2}\)
{m−1<4−2<2m+2⇔{m<5m>−2⇔−2<m<5A∩B⊂(−1;3)⇔{m−1≥−12m+2≤3⇔{m≥0m≤12⇔0≤m≤12m-1<4-2<2m+2⇔m<5m>-2⇔-2<m<5A∩B⊂(-1;3)⇔m-1≥-12m+2≤3⇔m≥0m≤12⇔0≤m≤12
Kết hợp với điều kiện (*) ta có 0 ≤ m ≤ 1/2 là giá trị cần tìm.
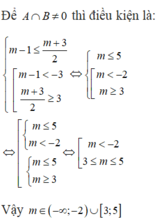
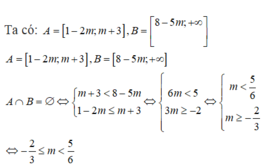
Để A ∪ B = A thì:
m - 5 < 2 và m + 1 ≥ 6
*) m - 5 < 2
⇔ m < 2 + 5
⇔ m < 7
*) m + 1 ≥ 6
⇔ m ≥ 6 - 1
⇔ m ≥ 5
Vậy 5 m < 7 thì A ∪ B = A