Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu tam giác ABC và A1B1C1 có cùng trọng tâm G thì \(\overrightarrow{AA_1}+\overrightarrow{BB_1}+\overrightarrow{CC_1}=\overrightarrow{0}\) bạn biết cái này chưa ?

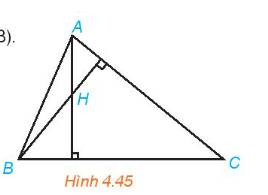
a) \( AH \bot BC\) và \(BH \bot CA\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \)
Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
b) Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH} = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)
Ta có: \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BC} = (8 - 8;8 - ( - 1)) = (0;9)\)
\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)
Lại có: \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \) và \(\overrightarrow {CA} = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)
\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)
Vậy H có tọa độ (6; 2)
c) Ta có: \(\overrightarrow {AB} = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}} = 3\sqrt {10} \)
Và \(\overrightarrow {BC} = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}} = 9\);
\(\overrightarrow {CA} = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}} = 3\sqrt {13} .\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)
\( \Rightarrow \widehat C \approx 56,{31^o}\)
Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)

Giải thích các bước giải:
a) Kẻ đường kính BF.
Ta có: AH⊥BC,CF⊥BC⇒AH//CFAH⊥BC,CF⊥BC⇒AH//CF
Lại có AF⊥AB,CH⊥AB⇒AF//CHAF⊥AB,CH⊥AB⇒AF//CH
⇒AHCF⇒AHCF là hình bình hành.
⇒−−→AH=−−→FC⇒AH→=FC→.
Lại có OIOI là đường trung bình của tam giác BCF nên −→OI=12−−→FCOI→=12FC→
Vậy −−→AH=−−→FC=2−→OIAH→=FC→=2OI→.
b) Ta có: −−→OH=−−→OA+−−→AH=−−→OA+2−→OI=−−→OA+−−→OB+−−→OCOH→=OA→+AH→=OA→+2OI→=OA→+OB→+OC→
c) Do GG là trọng tâm tam giác ABC nên−−→OA+−−→OB+−−→OC=3−−→OG⇒−−→OG=13(−−→OA+−−→OB+−−→OC)=13−−→OHOA→+OB→+OC→=3OG→⇒OG→=13(OA→+OB→+OC→)=13OH→
Vậy ba điểm O,H,GO,H,G thẳng hàng.

\(a,\) \(\overrightarrow{IA}=2\overrightarrow{IB}-4\overrightarrow{IC}\)
\(\overrightarrow{IA}=2\overrightarrow{IB}-2\overrightarrow{IC}-2\overrightarrow{IC}=2\overrightarrow{CB}-2\overrightarrow{IC}\)
\(=2\left(\overrightarrow{AB}-\overrightarrow{AC}\right)-2\left(\overrightarrow{AC}-\overrightarrow{AI}\right)\)
\(\overrightarrow{IA}=2\overrightarrow{AB}-2\overrightarrow{AC}-2\overrightarrow{AC}+2\overrightarrow{AI}\)
\(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}\)
\(b,\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}=\dfrac{4}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(1\right)\)
\(\overrightarrow{JG}=\overrightarrow{AG}-\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AM}-\dfrac{2}{3}\overrightarrow{AB}\)\((\) \(\) \(M\) \(trung\) \(điểm\) \(BC)\)
\(\overrightarrow{JG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}-\dfrac{2}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=-\dfrac{1}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\overrightarrow{IJ}=-4\overrightarrow{JG}\Rightarrow I,J,G\) \(thẳng\) \(hàng\)