Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Phương pháp:
Đặt z = a + b i , a , b ∈ R , giải tìm số phức z và tính tổng phần thực, phần ảo: a + b .
Cách giải:
Đặt z = a + b i , a , b ∈ R .
i z + 1 − i z ¯ = − 2 i ⇔ i a + b i + 1 − i a − b i = − 2 i ⇔ a i − b + a + b i − a i − b = − 2 i
⇔ − b i + a − 2 b = − 2 i ⇔ − b = − 2 a − 2 b = 0 ⇔ b = 2 a = 4 ⇒ a + b = 6
Tổng của phần thực và phần ảo là 6.

Đáp án D
![]()
Vậy phần thực và phần ảo của số phức z 1 . z 2 tương ứng là 4 và 0.
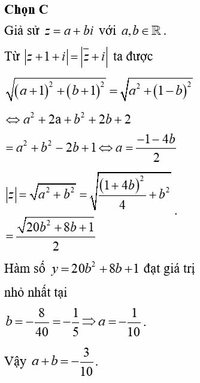
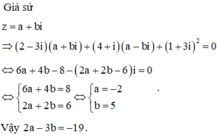
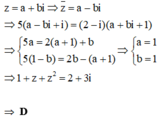
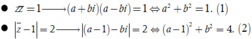
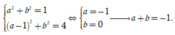

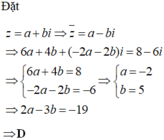
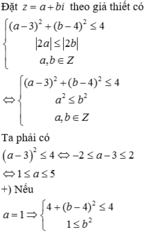
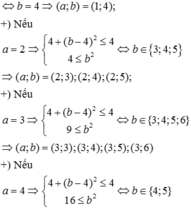


Chọn đáp án C
Ta có 2 z 1 z 2 = - 8 - 6 i
Số phức 2 z 1 z 2 có phần thực bằng -8 và phần ảo bằng -6