Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MÌnh học lớp 6 có gì sai bạn (chị anh) chỉ em nhé
Ta gọi 2 số đó là a;b
=> a+b=\(\sqrt{19}\)
=>a-b=\(\sqrt{17}\)
=> (a+b)2 - (a-b)2 = 19-17
=>a2+b2+2ab-a2-b2+2ab=2
=>4ab=2
=>ab=1/2
Vậy tích 2 số đó là 1/2


Đk: \(2\le x\le4\)
Áp dụng BĐT bunhiacopxki có:
\(P^2=\left(\sqrt{x-2}+3\sqrt{4-x}\right)^2\le\left(1+3^2\right)\left(x-2+4-x\right)\)
\(\Leftrightarrow P^2\le20\)\(\Leftrightarrow P\le2\sqrt{5}\)
Dấu "=" xảy ra khi \(\sqrt{x-2}=\dfrac{\sqrt{4-x}}{3}\) \(\Leftrightarrow x=\dfrac{11}{5}\) (tm đk)
Có \(P^2=8\left(4-x\right)+6\sqrt{\left(x-2\right)\left(4-x\right)}+2\ge2\)\(\Rightarrow P\ge\sqrt{2}\)
Dấu "=" xảy ra khi x=4 (tm)

I don't now
mik ko biết
sorry
......................

1.nhan xet
voi a thuoc Z
\(\left[\sqrt{a^2}\right]=\left[\sqrt{a^2+1}\right]=...=\left[\sqrt{a^2+2a}\right]\)
do do\(\left[\sqrt{a^2}\right]+\left[\sqrt{a^2+1}\right]+...+\left[\sqrt{a^2+2a}\right]=\frac{2a\left(2a+1\right)}{2}=a\left(2a+1\right)\)
thay a=1 cho den 10
tu tinh ra 825

Đề thì vừa đúng vừa sai. Đề đúng vì max cần tìm là có thật. Nhưng đề sai vì kết quả quá xấu (thậm chí đến WolframAlpha còn giải ko trọn vẹn mà chỉ ra xấp xỉ).
Ý tưởng thế này: Đặt \(X=\sqrt{x}\) thì \(\sqrt{y}=\frac{1}{X}\) nên viết lại biểu thức thành:
\(Q=\frac{1}{X+2}+\frac{1}{X+\frac{1}{X}+1}+\frac{1}{\frac{1}{X}+1}=\frac{X^4+5X^3+8X^2+6X+1}{\left(X+1\right)\left(X+2\right)\left(X^2+X+1\right)}\)
Tới đây có giải cũng ko được đâu, vì...
Theo WolframAlpha thì quả thật biểu thức có max nhưng giá trị đó là:
\(Q\approx1,20411\) tại \(X\approx1,75108\).
Khi mình tra sâu hơn về cái giá trị \(X\) trên kia thì nhận ra giá trị đó là nghiệm của pt
\(x^6+4x^5+5x^4-6x^3-22x^2-20x-7=0\) (giải kiểu gì???)
Mình nghĩ đề bài đã cho điều kiện x,y là hai số dương có tích bằng 1 thì nên áp dụng bất đẳng thức AM-GM sẽ phù hợp với chương trình lớp 9
cơ mà bạn tra sâu hơn về giá trị x như thế nào để biết x là nghiệm của phương trình trên :v tò mò quá
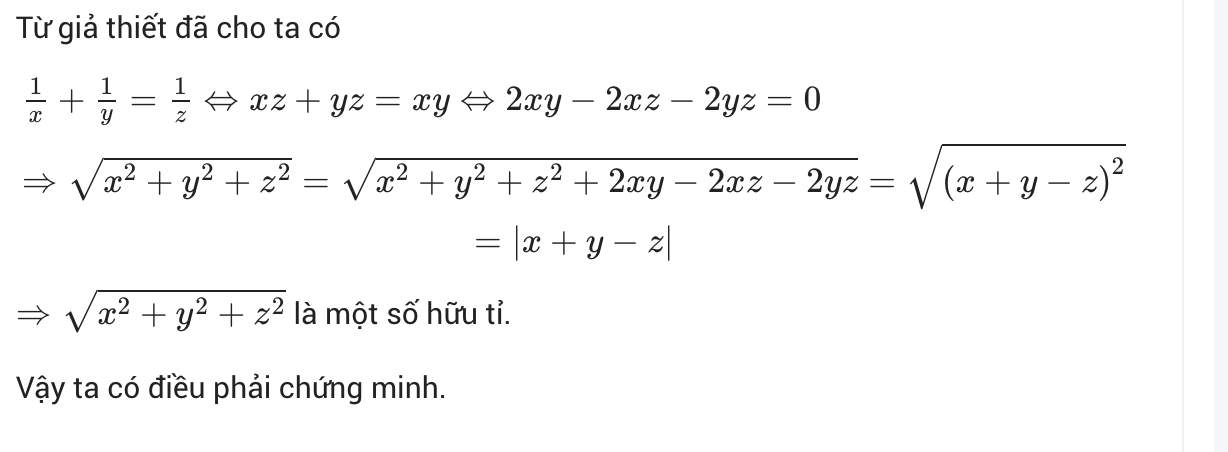
Gọi 2 số đó là a và b
Ta có: \(\left\{{}\begin{matrix}a+b=\sqrt{19}\\a-b=\sqrt{7}\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}a^2+2ab+b^2=19\\a^2-2ab+b^2=7\end{matrix}\right.\)
<=> \(\left(a^2+2ab+b^2\right)-\left(a^2-2ab+b^2\right)=19-7\)
<=> 4ab = 12
<=> ab = 3