Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.

a) Vì (P) // (Q), (R) cắt (P) suy ra (R) cũng cắt (Q).
b) a và b lần lượt là giao tuyến của (R) và các mp(P), (Q) do đó a và b đồng phẳng suy ra a và b không thể chéo nhau.
Mà a và b lần lượt thuộc hai mặt phẳng song song (P) và (Q) suy ra a // b.

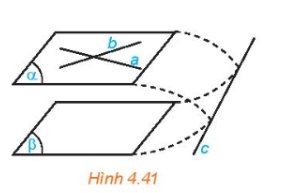
a) (Q) cắt (P) theo giao tuyến b suy ra b thuộc (Q).
Do đó a và b không thể chéo nhau.
b) Vì a // (P) và b thuộc (P) suy ra a và b không thể cắt nhau.

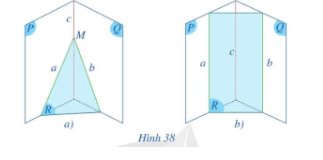
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

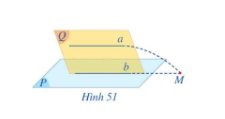
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.

a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
tham khảo
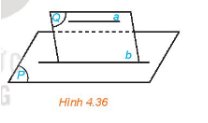
Ta có:\(a//\left(P\right)\)
\(a//\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=b\)
Do đó theo hệ quả định lí \(2\) ta có \(a//b\).

Đáp án A
Mặt phẳng ( α ) chứa điểm M và đường thẳng a
Mặt phẳng ( β ) chứa điểm M và đường thẳng b
Xét ( α ) và ( β ) có:
Điểm M là điểm chung
2 đường thẳng a và b chéo nhau
⇒ Tồn tại 1 giao tuyến duy nhất đi qua điểm M và cắt 2 đường thẳng a, b

Ta có (P) // (Q)
Suy ra AA’ // BB’ (1)
Ta có a // b
Suy ra AB // A’B’ (2)
Từ (1) và (2) suy ra AA’B’B là hình bình hành
Do đó AB = A’B’

M thuộc c suy ra M nằm trên mp(Q)
M thuộc a suy ra M nằm trên mp(R)
M cùng thuộc mp(R) và (Q) suy ra M nằm trên giao tuyến của mp(R) và (Q)
Như vậy , M thuộc b.