Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
![]()
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
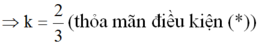
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:
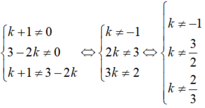
Vậy với ![]() thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

a, 2 đường thẳng // với nhau khi
\(\hept{\begin{cases}k+3=5-k\\2\ne3\end{cases}\Leftrightarrow k=1}\)
b, 2 đường thẳng cắt nhau khi
\(k+3\ne5-k\Leftrightarrow k\ne1\)
c, 2 đường thẳng trên ko thể trùng nhau được vì hệ số tự do 2 \(\ne\)3
Hàm số y = ( k + 1) x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = ( 3 – 2k ) x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là :
\(k+1\ne0\)và \(3-2k\ne0\)hay \(k\ne-1\)và \(k\ne\frac{3}{2}\)( * )
b) Hai đường thẳng y = ( k + 1 ) x + 3 và y = ( 3 – 2k ) x + 1 là hàm số bậc nhất nên \(a\ne0\) và \(a'\ne0\) Hai đường thẳng này cắt nhau khi \(a\ne a'\) tức là :
\(\hept{\begin{cases}k+1\ne0\\3-2k\ne\\k+1\ne3-2k\end{cases}0}\Leftrightarrow\hept{\begin{cases}k\ne-1\\2k\ne\\3k\ne2\end{cases}3}\Leftrightarrow\hept{\begin{cases}k\ne-1\\k\ne\\k\ne\frac{2}{3}\end{cases}\frac{3}{2}}\)
Với \(k\ne-1 ; k\ne\frac{3}{2} ; k\ne\frac{2}{3}\) thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do \(b\ne b'\) ( vì \(3\ne1\) ) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
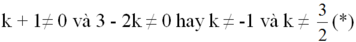
Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
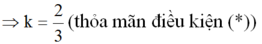

y = (k+1)x +3 (d)
và y = (3-2k)x + 1 (d’)
Các hàm số đã cho là hàm số bậc nhất khi:

a) Vì đã có 3 ≠ 1 nên (d) // (d’) khi và chỉ khi
k+1 = 3 – 2k
k = 2/3 (TMĐK (*))
Vậy với k = 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) song song với nhau.
b) Hai đường thẳng (d) cắt (d’) khi và chỉ khi k+1 ≠ 3 – 2k
k ≠ 2/3
Vậy với k ≠ -1, k ≠3/2 và k ≠ 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) cắt nhau.
c) Hai đường thẳng (d) và (d’) không thể trùng nhau vì có tung độ gốc khác nhau (do 3 ≠ 1).

b) Đồ thị hai hàm số y = (k + 3)x – 2 và y = (5 – k)x + 3 cắt nhau khi và chỉ khi:
k + 3 ≠ 5 - k ⇔ k ≠ 1
Kết hợp điều kiện với k ≠ 1; k ≠ -3 và k ≠ 5 thì đồ thị của hai hàm số đã cho cắt nhau.

a: Để hai đường này cắt nhau thì 2k+1<>k-1
=>k<>-2
b: Để hai đường song song thì 2k+1=k-1
=>k=-2
c: Hai đường này không thể trùng nhau được bởi vì b<>b'(3<>-4)

2:
a: Thay x=0 và \(y=\sqrt{2}\) vào y=2x+b, ta được:
\(b+2\cdot0=\sqrt{2}\)
=>\(b=\sqrt{2}\)
b: Thay x=-2 và y=-2 vào y=-4x+b,ta được:
b-4(-2)=-2
=>b+8=-2
=>b=-10
c: Vì (d)//y=-căn 3*x nên a=-căn 3
=>\(y=-\sqrt{3}\cdot x+b\)
Thay x=1 và \(y=3-\sqrt{3}\) vào (d),ta được:
\(b-\sqrt{3}=3-\sqrt{3}\)
=>b=3

a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)

Hai hàm số y = (k + 3) x - 2 và y = (5 - k)x + 3.
a) Đồ thị hai hàm số y = (k + 3)x – 2 và y = (5 – k)x + 3 là hai đường thẳng song song với nhau khi và chỉ khi:
Vậy k = 1 thì đồ thị của hai hàm số trên song song với nhau.