Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

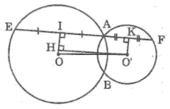
Kẻ OI ⊥ AE, O’K ⊥ AF
Trong đường tròn (O), ta có:
IA = IE = (1/2).AE (đường kính vuông góc với dây cung)
Trong đường tròn (O’), ta có:
KA = KF = (1/2).AF (đường kính vuông góc với dây cung)
Ta có: EF = AE = AF
Suy ra: EF = 2IA = 2AK = 2(IA + AK) = 2IK (1)
Kẻ O’H ⊥ OI
Khi đó tứ giác IHO’K là hình chữ nhật (có ba góc vuông)
Suy ra: O’H = IK
Trong tam giác OHO’ ta có: O’H ≤ OO’ = 3 (cm)
Suy ra: IK ≤ OO’ (2)
Từ (1) và (2) suy ra: EF ≤ 2OO’ = 6 (cm)
Ta có EF = 6cm khi H và O trùng nhau hay EF // OO’
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF // OO’

Mừng quá. Xong hết rồi. Hơn nửa tiếng bây giờ cũng được đền đáp =))
a) MB = MC (=MA) (giao điểm 2 tiếp tuyến cách đều tiếp điểm)
b) MA = MB = MC => T/g ABC vuông tại A => ^A = 90
T/g OAB cân tại O, có OM là đ/phân giác nên OM cũng là đ cao hay ^ANM = 90
Tương tự, ^APM = 90
=> đpcm
c) MO'/MO = O'C/BM (CMO' ~ BOM) = O'C/CM = CP/MP (CMO' ~ PMC) = MN/MP (PMC = NBM góc vuông - cạnh huyền - góc nhọn so le trong)
=> đpcm
d) Trong t/g vuông OMO' có MA là đường cao, OM^2 = OA.OO' <=> OM = 20 => BM = 12 (Pytago) => BC = 24
e) Dùng ta lét tìm ra OE, EC, còn OC tìm theo pytago trong t/g vuông OBC
f) ABKC là hình chữ nhật => AK cắt BC tại trung điểm M => đpcm

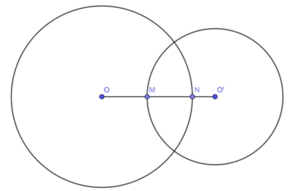
Ta có:
ON = 8cm, O'M = 6cm, OO' = 10cm
ON + O'M = OM + MN + MN + O'N = (OM + MN + O'N) + MN = OO' + MN
⇒ 8 + 6 = 10 + MN ⇒ MN = 4cm
Đáp án: D


độ dài \(OO'=20cm\)
Ta có: \(EF=OE+O'F-OO'\Rightarrow3=13+10-OO'\)
\(\Rightarrow OO'=20\)