Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

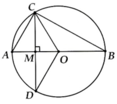
Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔACB vuông tại C
ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
=>IC=ID=CD/2=8cm
Xét ΔCAB vuông tại C cso CI là đường cao
nên CI^2=IA*IB
=>8^2=6*IB
=>IB=64/6=32/3(cm)
AB=IB+IA=32/3+6=50/3(cm)
=>R=50/3:2=25/3(cm)

a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2