Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Cách dựng (hình a):
- Dựng góc vuông xOy.
- Trên tia Ox, dựng đoạn OA = a
- Trên tia Oy, dựng đoạn OB = b.
- Nối AB, ta có đoạn AB = a 2 + b 2 cần dựng
*Chứng minh:
Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
A B 2 = O A 2 + O B 2 = a 2 + b 2
Suy ra: AB = a 2 + b 2


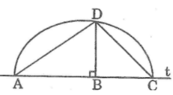
*Cách dựng:
- Dựng đường thẳng t.
- Trên đường thẳng t dựng liên tiếp hai đoạn thẳng AB = a, BC = b.
- Dựng nửa đường tròn tâm O đường kính AC.
- Từ B dựng đường thẳng vuông góc với AC cắt nửa đường tròn tâm O tại D
Ta có đoạn BD = a b cần dựng.
*Chứng minh:
Nối DA và DC. Ta có ΔACD vuông tại D và DB ⊥ AC.
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
B D 2 = AB.BC = a.b
Suy ra: BD = a b

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

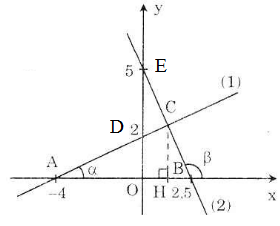
a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

Cách 1: Dựng hình vuông có số đo mỗi cạnh là 2. Ta có bình phương độ dài đường chéo của hình vuông đó là : 2^2 + 2^2 = 8
=> Đường chéo đó dài căn 8
Cách 2 Vẽ tam giác vuông cân có cạnh bên là 2 cm => cạnh huyền là căn 8


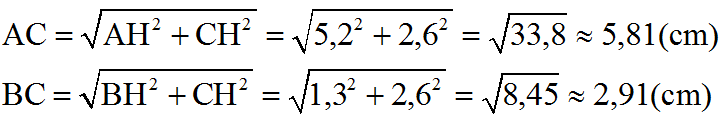

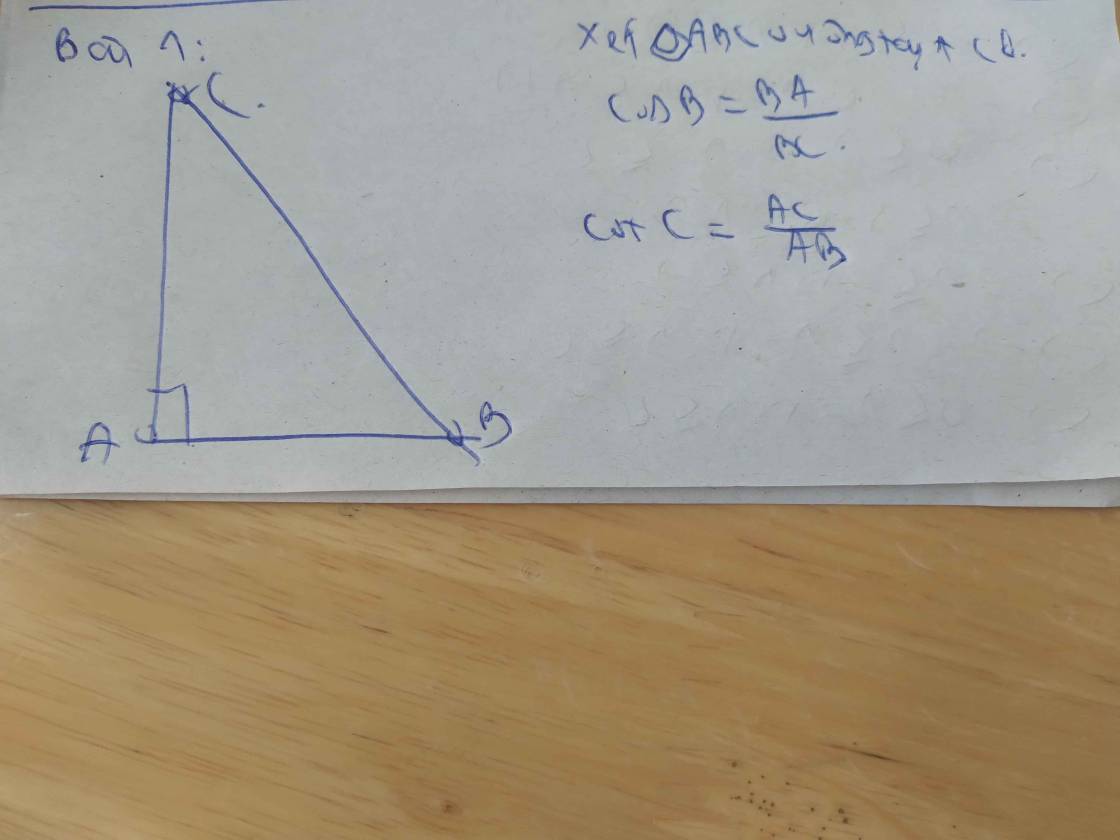

*Cách dựng (hình b):
- Dựng góc vuông xOy
- Trên tia Ox, dựng đoạn OA = b.
- Dựng cung tròn tâm A, bán kính bằng a cắt Oy tại B.
Ta có đoạn OB = a 2 - b 2 ( a > b ) cần dựng.
*Chứng minh:
Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
A B 2 = O A 2 + O B 2 ⇒ O B 2 = A B 2 - O A 2 ⇒ a 2 - b 2
Suy ra: OB = a 2 - b 2