Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
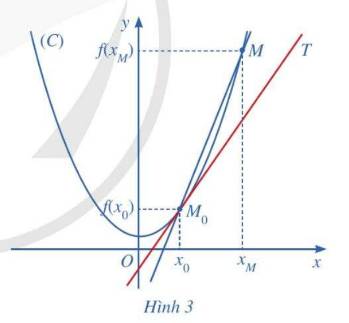
a) \({k_0} = \mathop {\lim }\limits_{x \to {x_M}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = f'({x_0})\)
b) Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):
\(y = {k_0}(x - {x_0}) + {y_0}\)
\(y'=3x^2-6x\)
Do M thuộc (C) nên hệ số góc của tiếp tuyến tại M:
\(k=f\left(a\right)=3a^2-6a\)
\(f'\left(a\right)=6a-6>0;\forall a\in\left[2;3\right]\)
\(\Rightarrow f\left(a\right)\) đồng biến trên \(\left[2;3\right]\Rightarrow k_{max}\) khi \(a=3\)
\(\Rightarrow b=a^3-3a^2-1=-1\)
\(S=3-1=2\)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
a: \(y=-x^2+3x-2\)
=>\(y'=-\left(2x\right)+3\cdot1\)
=>y'=-2x+3
=>\(f'\left(x_0\right)=-2\cdot x_0+3\)
b: \(f'\left(2\right)=-2\cdot2+3=-4+3=-1\)
\(f\left(2\right)=-2^2+3\cdot2-2=0\)
Phương trình tiếp tuyến của (P) tại điểm có hoành độ x=2 là:
\(y-f\left(2\right)=f'\left(2\right)\left(x-2\right)\)
=>\(y-0=-1\left(x-2\right)=-x+2\)
=>y=-x+2
c: Đặt y=0
=>\(-x^2+3x-2=0\)
=>\(x^2-3x+2=0\)
=>(x-2)(x-1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
TH1: x=2
\(f'\left(2\right)=-2\cdot2+3=-1;f\left(2\right)=-2^2+3\cdot2-2=0\)
Phương trình tiếp tuyến tại điểm có hoành độ x=2 là:
y-f(2)=f'(2)(x-2)
=>y-0=-1(x-2)
=>y=-x+2
TH2: x=1
\(f'\left(1\right)=-2\cdot1+3=1\)
f(1)=0
Phương trình tiếp tuyến tại điểm có hoành độ x=1 là:
y-f(1)=f'(1)(x-1)
=>y-0=1(x-1)
=>y=x-1
d: Gọi phương trình tiếp tuyến cần tìm là (d): y=ax+b(a<>0)
Vì (d) vuông góc với y=x+3 nên a*1=-1
=>a=-1
=>y=-x+b
=>f'(x)=-1
=>-2x+3=-1
=>-2x=-4
=>x=2
f(2)=-2^2+3*2-2=0
f'(2)=-1
Phương trình tiếp tuyến là:
y-f(2)=f'(2)(x-2)
=>y-0=-1(x-2)
=>y=-x+2
a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)
- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm.
- Ta có:
- Vậy phương trình tiếp tuyến cần tìm là :
Chọn A