Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\begin{array}{l}\lim {u_n} = \lim \left( {3 + \frac{1}{n}} \right) = \lim 3 + \lim \frac{1}{n} = 3 + 0 = 3\\\lim {v_n} = \lim \left( {5 - \frac{2}{{{n^2}}}} \right) = \lim 5 - \lim \frac{2}{{{n^2}}} = 5 - 0 = 5\end{array}\)
b)
\(\begin{array}{l}\lim \left( {{u_n} + {v_n}} \right) = \lim {u_n} + \lim {v_n} = 3 + 5 = 8\\\lim \left( {{u_n} - {v_n}} \right) = \lim {u_n} - \lim {v_n} = 3 - 5 = - 2\\\lim \left( {{u_n}.{v_n}} \right) = \lim {u_n}.\lim {v_n} = 3.5 = 15\\\lim \frac{{{u_n}}}{{{v_n}}} = \frac{{\lim {u_n}}}{{\lim {v_n}}} = \frac{3}{5}\end{array}\)

a) \({v_n} = {u_n} - 2 = \frac{{2n + 1}}{n} - 2 = \frac{{2n + 1 - 2n}}{n} = \frac{1}{n}\).
Áp dụng giới hạn cơ bản với \(k = 1\), ta có: \(\lim {v_n} = \lim \frac{1}{n} = 0\).
b) \({u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}\)
Biểu diễn trên trục số:
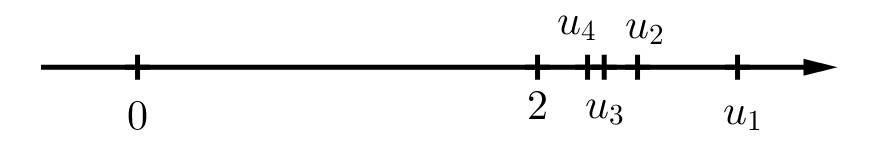
Nhận xét: Điểm \({u_n}\) càng dần đến điểm 2 khi \(n\) trở nên rất lớn.

\(limu_n=lim\dfrac{1}{n}=0\); \(limv_n=lim\left(-\dfrac{1}{n}\right)=0\).
\(limf\left(u_n\right)=lim\left(\sqrt{\dfrac{1}{n}}+1\right)=1\).
\(limf\left(v_n\right)=lim\left(2.\dfrac{-1}{n}\right)=lim\dfrac{-2}{n}=0\).
Hai dãy số \(\left(u_n\right)\) và \(\left(v_n\right)\) đều có giới hạn 0 khi n tiến ra dương vô cùng nhưng \(limf\left(u_n\right)\ne limf\left(v_n\right)\) nên f không có giới hạn tại \(x=0\).

a) Ta có: \({u_{n + 1}} = 3\left( {n + 1} \right) - 1 = 3n + 2\).
Suy ra \({u_{n + 1}} > {u_n}\).
b) Ta có: \({v_{n + 1}} = \frac{1}{{{{\left( {n + 1} \right)}^2}}}\).
Suy ra: \({u_{n + 1}} < {u_n}\).

a) Vì \(\lim \left( {8 + \frac{1}{n} - 8} \right) = \lim \frac{1}{n} = 0\) nên \(\lim {u_n} = 8.\)
Vì \(\lim \left( {4 - \frac{2}{n} - 4} \right) = \lim \frac{{ - 2}}{n} = 0\) nên \(\lim {v_n} = 4.\)
b) \({u_n} + {v_n} = 8 + \frac{1}{n} + 4 - \frac{2}{n} = 12 - \frac{1}{n}\)
Vì \(\lim \left( {12 - \frac{1}{n} - 12} \right) = \lim \frac{{ - 1}}{n} = 0\) nên \(\lim \left( {{u_n} + {v_n}} \right) = 12.\)
Mà \(\lim {u_n} + \lim {v_n} = 12\)
Do đó \(\lim \left( {{u_n} + {v_n}} \right) = \lim {u_n} + \lim {v_n}.\)
c) \({u_n}.{v_n} = \left( {8 + \frac{1}{n}} \right).\left( {4 - \frac{2}{n}} \right) = 32 - \frac{{14}}{n} - \frac{2}{{{n^2}}}\)
Sử dụng kết quả của ý b ta có \(\lim \left( {32 - \frac{{14}}{n} - \frac{2}{{{n^2}}}} \right) = \lim 32 - \lim \frac{{14}}{n} - \lim \frac{2}{{{n^2}}} = 32\)
Mà \(\left( {\lim {u_n}} \right).\left( {\lim {v_n}} \right) = 32\)
Do đó \(\lim \left( {{u_n}.{v_n}} \right) = \left( {\lim {u_n}} \right).\left( {\lim {v_n}} \right).\)