NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
30 tháng 10 2016
A = (4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6) + (4^7 + 4^8 + 4^9 + 4^10 + 4^11 + 4^12) + (4^13 + 4^14 + 4^15 + 4^16 + 4^17 + 4^18) + (4^19 + 4^20 + 4^21 + 4^22 + 4^23 + 4^24)
A = (4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6) + 4^6(4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6) + 4^12(4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6) + 4^18(4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6)
A = (4 + 4^2 + 4^3 + 4^4 + 4^5 + 4^6).(1+4^6+4^12+4^18)
A = 5460.(1+4^6+4^12+4^18)
A = 420 . 13(1+4^6+4^12+4^18) => A chia hết cho 420
A = 20.21.13(1+4^6+4^12+4^18) => A chia hết cho 20 ; 21
TH
1
DT
1
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
$A=(4+4^2)+(4^3+4^4)+....+(4^{23}+4^{24})$
$=(4+4^2)+4^2(4+4^2)+....+4^{22}(4+4^2)$
$=(4+4^2)(1+4^2+...+4^{22})$
$=20(1+4^2+...+4^{22})\vdots 20$
----------------------------
$A=(4+4^2+4^3)+(4^4+4^5+4^6)+....+(4^{22}+4^{23}+4^{24})$
$=4(1+4+4^2)+4^4(1+4+4^2)+....+4^{22}(1+4+4^2)$
$=(1+4+4^2)(4+4^4+...+4^{22})$
$=21(4+4^4+....+4^{22})\vdots 21$
----------------------
Vậy $A\vdots 20; A\vdots 21$. Mà $(20,21)=1$ nên $A\vdots (20.21)$ hay $A\vdots 420$
9 tháng 9 2015
\(A=\left(4+4^2\right)+.......+\left(4^{23}+4^{24}\right)\)
\(A=20.1+20.2^4+.......+20.2^{24}\)
\(A=20.\left(1+2^4+..........+2^{24}\right)\)
Vậy A chia hết cho 20
\(A=\left(4+4^2+4^3\right)+........+\left(4^{22}+4^{23}+4^{24}\right)\)
\(A=4.21+4^4.21+......+4^{20}.21\)
\(A=21.\left(1+4^4+......+4^{20}\right)\)
Vậy A chia hết cho 21
\(A=\left(4+4^2+......+4^6\right)+.........+\left(4^{19}+4^{20}+4^{21}+4^{22}+4^{23}+4^{24}\right)\)\(A=13.420+4^6.13.420+........+4^{18}.13.420\)
\(A=420.13.\left(1+4^6+4^{12}+4^{18}\right)\)
Vậy A chia hết cho 420
NT
6
2 tháng 8 2015
Ta có:
A = 4 + 42 + 43 +......+ 423+ 424
= (4 + 42)) + (43 +44)......+ (423+ 424)
=(4 + 42).1+(4 + 42).42+...+(4 + 42).422
=20.(1+42+...+422) chia hết cho 20
Ta lại có:
A = 4 + 42 + 43 +......+ 423+ 424
=(4 + 42 + 43)+...+(422+423+424)
=(4 + 42 + 43).1+...+(4 + 42 + 43).421
=21.(1+...+421) chia hết cho 21
Vì A chia hết cho 21 và 20 , mà ƯCLN(20;21)=1 => A chia hết cho 20 và 21 tức là A chia hết cho 20.21=420
Vậy...
3 tháng 8 2016
A = 4 + 42 + 43 +......+ 423+ 424
Ta thấy các cặp số liên tiếp cộng lại với nhau đều chia hết cho 20, ví dụ:
4 + 42 = 20, 43 + 44 = 320, 45 + 46 = 5120...
Vì đây là số chẵn, nên A sẽ chia hết cho 20.
Tiếp tục, BC (21 và 4) = {84; 168; 252; 336; 420; 504; 588....}
Như vậy, ta để ý thấy tích của các lũy thừa gồm số 4 và số mũ đều là số chẵn, BC của 4 và 21 cũng đều là số chẵn.
Vậy A chia hết cho 21.
Song, vì A chia hết cho 20 và 21, trong trường hợp này A chỉ có thể chia hết cho 20.21 = 420
O
0
AP
2
KV
20 tháng 12 2023
A = 4 + 4² + 4³ + ... + 4²³ + 4²⁴
Số số hạng của A:
24 - 1 + 1 = 24
Do 24 ⋮ 2 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 2 số hạng như sau:
A = (4 + 4²) + (4³ + 4⁴) + ... + (4²³ + 4²⁴)
= 20 + 4².(4 + 4²) + ... + 4²².(4 + 4²)
= 20 + 4².20 + ... + 4²².20
= 20.(1 + 4² + ... + 4²²) ⋮ 20
Vậy A⋮ 20 (1)
Do 24 ⋮ 3 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
A = (4 + 4² + 4³) + (4⁴ + 4⁵ + 4⁶) + ... + (4²² + 4²³ + 4²⁴)
= 4.(1 + 4 + 4²) + 4⁴.(1 + 4 + 4²) + ... + 4²².(1 + 4 + 4²)
= 4.21 + 4⁴.21 + ... + 4²².21
= 21.(4 + 4⁴ + ... + 4²²) ⋮ 21
Vậy A ⋮ 21 (2)
Từ (1) và (2) ⇒ A ⋮ 20 . 21 (do 20 và 21 nguyên tố cùng nhau)
⇒ A ⋮ 420
Vậy A chia hết cho 20; 21; 420
6 tháng 6 2018
a/ Ta có :
\(A=4+4^2+.....+4^{23}+4^{24}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+....+\left(4^{23}+4^{24}\right)\) (12 nhóm)
\(=4\left(4+4^2\right)+4^3\left(4+4^2\right)+.......+4^{23}\left(4+4^2\right)\)
\(=4.20+4^3.20+.....+4^{23}.20\)
\(=20\left(4+4^3+...+4^{23}\right)⋮20\)
\(\Leftrightarrow A⋮20\left(đpcm\right)\)
b/ Ta có :
\(A=4+4^2+4^3+........+4^{23}+4^{24}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+.......+\left(4^{22}+4^{23}+4^{24}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+....+4^{22}\left(1+4+4^2\right)\)
\(=4.21+4^4.21+....+4^{22}.21\)
\(=21\left(4+4^4+......+4^{22}\right)⋮21\)
\(\Leftrightarrow A⋮21\left(đpcm\right)\)
V
6 tháng 6 2018
*A chia hết cho 20 : A có 24 lũy thừa.
Trước hết ta thấy rõ A chia hết cho 4 vì từng số hang của dãy số A chia hết cho 4
A có 24 lũy thừa nên ta chia thành 12 cặp lũy thừa
A = (4+4^2) + (4^3+4^4) + ...+ (4^23+4^24)
A = 4.(1+4) + 4^3.(1+4) + ...+ 4^23.(1+4)
A = 4.5 + 4^3.5 + .....+ 4^23.5
vậy A chia hết cho 5 và 4 nên A chia hết cho 20
*A chia hết cho 21 : A có 24 lũy thừa
Nhóm thành mỗi nhóm 3 lũy thừa ta được 8 nhóm lũy thừa
A = 4.(1+4+4^2) + ......+ 4^22.(1+4+4^2)
A = 4.21 + ......+4^22.21 => A chia hết 21
Vậy A chia hết cho 21.
*A chia hết cho 420 .
Ta có : A chia hết cho 20 và 21 mà 20 và 21 là nguyên tố cùng nhau nên
A chia hết cho 20.21 = 420 (Áp dụng: Một số đồng thời chia hết cho cả m và n. m và n đồng thời chỉ chia hết cho 1 và chính nó thì số đó chia hết cho tích mxn)
Vậy A chia hết cho 420 .
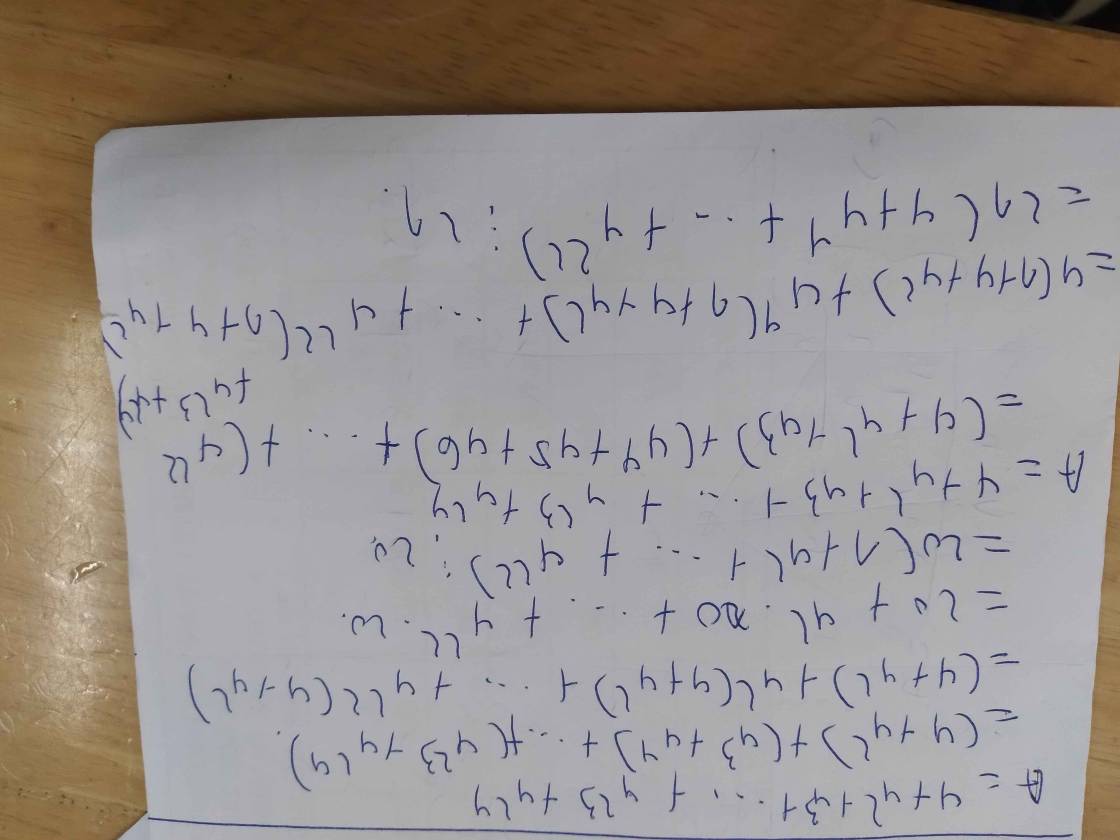
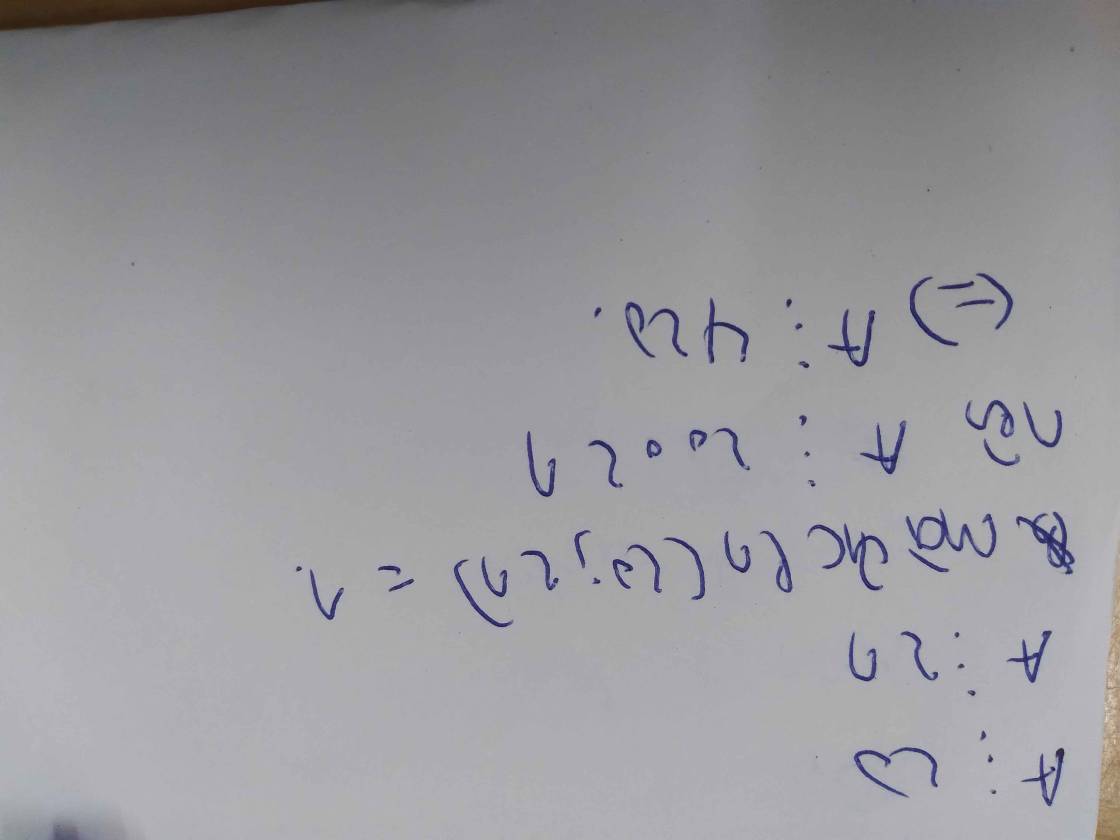
Ta có
H=4+4^2+...+4^24
H=(4+4^2) + (4^3+4^4)+...+(4^23+4^24)
<=>H=20+4^2.20+...+4^22.20
<=>h=20(1+4^2+...+4^22) chia hết cho 20
Ta có
H=4 +4^2+...+4^24
<=>H=(4+4^2+4^3) +(4^4+4^5+4^6)+....+(4^22+4^23+4^24)
<=>H=4.21+4^4.21+....+4^22 .21
<=>H=21(4+4^4+...+4^22) chia hết cho 21
H=4+4^2+...+4^2
<=>h=(4+4^2+4^3+4^4+4^5+4^6)+....+(4^19+4^20+4^21+4^22+4^23+4^24)
=5420 + ...+4^18.5420
=13.420 +....+13.420.4^18
chia hết cho 420
nhớ tick mình nha,cảm ơn nhiều
Ta có:
A = 4 + 42 + 43 +......+ 423+ 424
= (4 + 42)) + (43 +44)......+ (423+ 424)
=(4 + 42).1+(4 + 42).42+...+(4 + 42).422
=20.(1+42+...+422) chia hết cho 20
Ta lại có:
A = 4 + 42 + 43 +......+ 423+ 424
=(4 + 42 + 43)+...+(422+423+424)
=(4 + 42 + 43).1+...+(4 + 42 + 43).421
=21.(1+...+421) chia hết cho 21
Vì A chia hết cho 21 và 20 , mà ƯCLN(20;21)=1 => A chia hết cho 20 và 21 tức là A chia hết cho 20.21=420
Vậy...