Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABO vuông tại B và ΔACO vuông tại C có
OA chung
\(\widehat{BOA}=\widehat{COA}\)
Do đó: ΔABO=ΔACO
Suy ra: AB=AC
hay ΔABC cân tại A
mà \(\widehat{CAB}=180^0-120^0=60^0\)
nên ΔABC đều

Bài này mình biết làm nhưng không biết vẽ hình trên máy tính

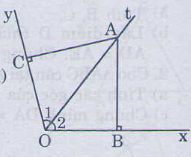
Hai tam giác vuông ACO và ABO có:
ˆO1O1^=ˆO2O2^(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).

Hai tam giác vuông ACO và ABO có:
=(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).

Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)

Xét \(\Delta ABO\) và \(\Delta ACO\) có :
Góc ABO = Góc ACO ( = 90* )
AO là cạnh huyền chung của 2 tam giác
Góc AOB = Góc AOC ( OA là p/g góc xOy )
=> \(\Delta ABO=\Delta ACO\) ( cạnh huyền - góc nhọn )
=> AB=AC
Vì AB=AC => Tam giác ABC là tam giác cân .
Tick nha !