Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) Xét \(\Delta OAD,\Delta OCB\) có:
\(OA=OC\left(gt\right)\)
\(\widehat{O}\): góc chung
\(OD=OB\left(gt\right)\)
\(\Rightarrow\Delta OAD=\Delta OCB\left(c-g-c\right)\)
\(\Rightarrow AD=CB\) ( cạnh t/ứng )
\(\Rightarrow\widehat{B_1}=\widehat{D_1}\) ( góc t/ứng )
b) Ta có: OB = OD
OA = OC
\(\Rightarrow OB-OA=OD-OC\)
\(\Rightarrow AB=CD\)
Ta có: \(\widehat{A_1}+\widehat{B_1}+\widehat{E_1}=180^o\)
\(\widehat{C_1}+\widehat{E_2}+\widehat{D_1}=180^o\)
Mà \(\widehat{B_1}=\widehat{D_1}\) ( theo phần a ); \(\widehat{E_1}=\widehat{E_2}\) ( đối đỉnh )
\(\Rightarrow\widehat{A_1}=\widehat{C_1}\)
Xét \(\Delta EAB,\Delta ECD\) có:
\(\widehat{A_1}=\widehat{C_1}\left(cmt\right)\)
AB = CB ( cmt )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(\Rightarrow\Delta EAB=\Delta ECD\left(g-c-g\right)\)
\(\Rightarrow EB=ED\) ( cạnh t/ứng )
c) Xét \(\Delta OBE,\Delta ODE\) có:
\(EB=ED\) ( theo phần b )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(OB=OD\left(gt\right)\)
\(\Rightarrow\Delta OBE=\Delta ODE\left(c-g-c\right)\)
\(\Rightarrow\widehat{O_1}=\widehat{O_2}\)
\(\Rightarrow OE\) là tia phân giác của \(\widehat{xOy}\)
Vậy...
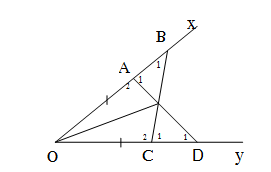

Giải:
a) ∆OAD và ∆OCB có:
OA= OC(gt)
∠O chung OB = OD (gt)
OAD = OCB (c.g.c) AD = BC
Nên ∆OAD=∆OCB (c.g.c) => AD=BC.
b) Ta có
∠A1 = 1800 – ∠A2
∠C1 = 1800 – ∠C2
∠A2 = ∠C2 do ΔOAD = ΔOCB (c/m trên)
⇒ ∠A1 = ∠C1
Ta có:
OB = OA + AB
OD = OC + CD
mà OB = OD, OA = OC
⇒ AB = CD
Xét ΔEAB = ΔECD có:
∠A1 = ∠C1 (c/m trên)
AB = CD (c/m trên)
∠B1 = ∠D1 (ΔOCB = ΔOAD)
⇒ ΔEAB = ΔECD (g.c.g)
c) Xét ΔOBE và ΔODE có:
OB = OD (GT)
OE chung
AE = CE (ΔAEB = ΔCED)
⇒ΔOBE = ΔODE (c.c.c)
⇒ ∠AOE = ∠COE
⇒ OE là phân giác của góc ∠xOy.

a/ Xét t/g OAD và t/g OBC cos
AO = OB
\(\widehat{xOy}\) : chung
OD = OC
=> t/g OAD = t/g OBC
=> AD = BC
b/ Không rõ đề.
c/ Có
OC = ODOA = OB
=> AC = BD
Có \(\widehat{OAD}=\widehat{OBE}\) (do t/g OAD = t/g OBC)
=> \(180^o-\widehat{OAD}=180^o-\widehat{OBE}\)
=> \(\widehat{CAD}=\widehat{CBD}\)
Xét t/g AEC và t/g BED có
\(\widehat{CAD}=\widehat{CBD}\)
AC = BD\(\widehat{OCB}=\widehat{ODA}\)
=> t/g AEC = t/g BED (g.c.g)
=> AE = BE
Xét t/g OAE và t/g OBE có
OA = OB
AE = BEOE : chung
=> t/g OAE = t/g OBE
=> ^xOE = ^yOe
=> OE là pg góc xOy


