K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
nhận giá trị là số nguyên.
20 tháng 7 2021
a) Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\left(\sqrt{x}+1\right)\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
17 tháng 9 2021
\(M=a^2+ab+b^2-3a-3b+2001\)
\(\Rightarrow2M=2a^2+2ab+2b^2-6a-6b+4002\)
\(=\left[\left(a+b\right)^2-2\left(a+b\right).2+4\right]+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+3996\)
\(=\left(a+b-2\right)^2+\left(a-1\right)^2+\left(b-1\right)^2+3996\ge3996\)
\(\Rightarrow M\ge1998\)
\(minM=1998\Leftrightarrow a=b=1\)
NH
1
13 tháng 6 2021
\(T=\)\(\dfrac{x^2+x+7}{x-1}=\dfrac{\left(x+2\right)\left(x-1\right)+9}{x-1}=x+2+\dfrac{9}{x-1}\)
\(=\left(x-1+\dfrac{9}{x-1}\right)+3\ge2\sqrt{\dfrac{9}{x-1}.\left(x-1\right)}+3\)\(=\)\(9\)
\(\Leftrightarrow T_{min}=9\Leftrightarrow x-1=\dfrac{9}{x-1}\Leftrightarrow x=4\)
VT
1
16 tháng 8 2023
`\sqrt{x^2 - 2x + 4}`
`=\sqrt{(x-1)^2 + 3}`
Do `\sqrt{(x-1)^2 + 3} >=0`
`(x-1)^{2} >=0`
`=>(x-1)^{2} + 3 >=3AAx`
`=>\sqrt{(x-1)^2 + 3} >= \sqrt{3}AAx`
Dấu "=" xảy ra `<=>x-1=0`
`<=>x=1`
Vậy `min` của biểu thức là `\sqrt{3} <=>x=1`
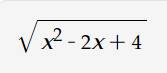
Áp dụng BDT Bunhiacopki, ta có
\(1^2\le\left(x+3y\right)^2\le\left(1^2+3^2\right)\left(X^2+Y^2\right)\)
\(\Rightarrow\)\(X^2+Y^2\)\(\ge\frac{1}{10}\).Dấu bằng xảy ra
\(\Leftrightarrow x=3y\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{3}{10}\\y=\frac{1}{10}\end{cases}}\)