Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`@` `\text {dnammv}`
`a,`
`M(x)=3x^3+x^2+4x^4-x-3x^3+5x^4+x^2`
`= (4x^4+5x^4)+(3x^3-3x^3)+(x^2+x^2)-x`
`= 9x^4+2x^2-x`
`N(x)=-x^2-x^4+4x^3-x^2-5x^3+3x+1+x`
`=-x^4+(4x^3-5x^3)+(-x^2-x^2)+(3x+x)+1`
`= -x^4-x^3-2x^2+4x+1`
`b,`
`M(x)+N(x)=(9x^4+2x^2-x)+(-x^4-x^3-2x^2+4x+1)`
`= 9x^4+2x^2-x-x^4-x^3-2x^2+4x+1`
`= (9x^4-x^4)-x^3+(2x^2-2x^2)+(-x+4x)+1`
`= 8x^4-x^3+3x+1`
`N(x)-M(x)=(-x^4-x^3-2x^2+4x+1)-(9x^4+2x^2-x)`
`= -x^4-x^3-2x^2+4x+1-9x^4-2x^2+x`
`= (-x^4-9x^4)-x^3+(-2x^2-2x^2)+(4x+x)+1`
`= -10x^4-x^3-4x^2+5x+1`
`c,`
`P(x)=M(x)+N(x)`
`P(x)= 8x^4-x^3+3x+1`
Thay `x=-2`
`P(-2)= 8*(-2)^4-(-2)^3+3*(-2)+1`
`= 8*16+8-6+1`
`= 136-6+1=131`

\(\dfrac{X}{Y}=\dfrac{7}{5}x^{n-1}-x^{3-n}\)
Để X chia hết cho Y thì n-1>=0 và 3-n>=0
=>1<=n<=3
=>\(n\in\left\{1;2;3\right\}\)

A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49

Ta có :
\(f\left(x\right)-g\left(x\right)=x^{2n}-x^{2n-1}+...+x^2-x+1-\left(-x^{2n+1}+x^{2n}-x^{2n-1}+...+x^2-x+1\right)\)
\(\Rightarrow f\left(x\right)-g\left(x\right)=x^{2n}-x^{2n-1}+...+x^2-x+1+x^{2n+1}-x^{2n}+x^{2n-1}+...-x^2+x-1\)
\(\Rightarrow f\left(x\right)-g\left(x\right)=x^{2n+1}+\left(x^{2n}-x^{2n}\right)+\left(x^{2n-1}-x^{2n-1}\right)+...+\left(x^2-x^2\right)+\left(x-x\right)\)+ ( 1 - 1 )
\(\Rightarrow f\left(x\right)-g\left(x\right)=x^{2n+1}\)
Thay \(x=\frac{1}{10}\)vào \(f\left(x\right)-g\left(x\right)\)ta được :
\(\left(\frac{1}{10}\right)^{2n+1}=\left(\frac{1}{10}\right)^{2n}.\frac{1}{10}=\left(\frac{1^2}{10^2}\right)^n.\frac{1}{10}=\left(\frac{1}{100}\right)^n.\frac{1}{10}=\frac{1}{100^n}.\frac{1}{10}\)
Vậy \(f\left(x\right)-g\left(x\right)=\frac{1}{100^n}.\frac{1}{10}\)

* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
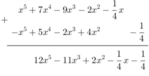
* f(x) - g(x)
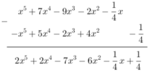

a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
Câu hỏi của Công Chúa Của Những Vì Sao - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé! Hai bài làm tương tự nhau:)