Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp

\(f'\left(x\right)=-2cosx.sinx-2sinx.cosx=-2sin2x\)
\(\Rightarrow f'\left(\frac{\pi}{4}\right)=-2sin\left(\frac{2\pi}{4}\right)=-2sin\left(\frac{\pi}{2}\right)=-2\)

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)

d.
\(\Leftrightarrow\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=0\)
\(\Leftrightarrow sin^2x-cos^2x=0\)
\(\Leftrightarrow-cos2x=0\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
e. Đề thiếu
f.
\(\Leftrightarrow sin2x=\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)\left(cos^2\frac{x}{2}+sin^2\frac{x}{2}\right)\)
\(\Leftrightarrow sin2x=cos^2\frac{x}{2}-sin^2\frac{x}{2}\)
\(\Leftrightarrow sin2x=cosx\)
\(\Leftrightarrow sin2x=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-x+k2\pi\\2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
a.
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\sqrt{2}>1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
b.
\(\Leftrightarrow sin2x=1\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
c.
\(\Leftrightarrow2sin2x.cos2x=-1\)
\(\Leftrightarrow sin4x=-1\)
\(\Leftrightarrow4x=-\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{\pi}{8}+\frac{k\pi}{2}\)

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0
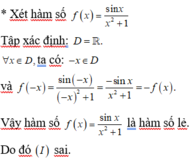
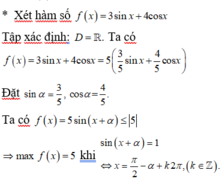

Ta có:
f ' x = 2 cos x cos x ' − 2 sin x sin x '
= − 2 cos x sin x − 2 sin x cos x = − 4 sin x cos x = − 2 sin 2 x .
⇒ f ' π 4 = − 2 sin 2 π 4 = − 2 sin π 2 = − 2.
Chọn đáp án A