K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NG
3
11 tháng 9 2023
Bạn bấm vào nút "đúng" thôi.
Riêng trường hợp giáo viên, cộng tác viên nhấn "đúng" cho câu trả lời thì sẽ có 1-2 GP
29 tháng 9 2015
để hàm số f có cực trị tại a thì f'(\(x_0\))=0
để tìm cực trị của hàm số thì có 2 quy tắc
1, quy tắc 1
f liên tục trên (a,b) chữa điểm a và có đạo hàm trên các khoảng (a;\(x_0\)) và (\(x_0\),b). Khi đó
a, nếu f'(x)<0 với mọi \(x\in\) (a;\(x_0\)) và f'(\(x_0\))>0 với mọi \(x\in\left(x_0;b\right)\) thì hàm số f đạt cực tiểu tại điểm \(x_0\)
b, nếu f'(x)>0 với mọi \(x\in\) (a;\(x_0\)) và f'(\(x_0\))<0 với mọi \(x\in\left(x_0;b\right)\) thì hàm số f đạt cực đại tại điểm \(x_0\)
quy tắc 1
bước 1. tìm f'(x)
bước 2:tìm các điểm \(x_i\) tại đó đạo hàm của nó =0 hoặc hàm số liên tục nhưng ko có đạo hàm
bước 3: xét dấu f'(x). nếu f'(x) đổi dấu khi qua điểm xi thì hàm số đặt cực trị tại xi
Gỉa sử f có đạo hàm cấp 1 trên khoảng (a,b) chứa điểm x0 , f'(x0)=0 f có đạo hàm cấp hai khác 0 tại điểm x0
a, nếu f''(x0)<0 thì hàm số đạt cực đại tại x0
b, nếu f''(x0)>0 thì hàm số đạt cực tiểu tại x0
quy tắc 2:
bước 1: tìm f'(x)
tìm các nghiệm của phương trình f'(xi)=0
bước 3: tìm f''(x) và tính f''(xi)
nếu f''(xi)<0 thì hàm số đạt cực đại tại xi
nếu f''(xi)>0 thì hàm số đạt cực đại tại xi
MT
2
LN
Lưu Nguyễn Hà An
CTVHS
25 tháng 1
Bn kiếm GP giống SP thôi, nhưng mà bạn cần trả lời hay thì mới đc các thầy cô tick cho nhé!
16 tháng 4 2016
Không
VD:
Tìm tỉ số của 5 và 8 ta lấy:
5 : 8 = \(\frac{5}{8}\)
Giống với phân số \(\frac{5}{8}\)
CM
25 tháng 11 2018
Ta có BXD của f ' x như sau:
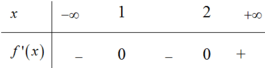
Dựa vào BXD ta có:
Hàm số nghịch biến trên - ∞ ; 1 và 1 ; 2 đồng biến trên 2 ; + ∞
Dựa vào đồ thị của hàm số y = f ' x ta thấy f ' x đồng biến trên khoảng 2 ; + ∞ ⇒ y = f x đồng biến trên 2 ; + ∞
Chọn B.
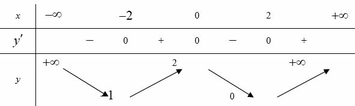
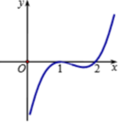
bấm vào biểu tượng fx ý rồi thao hồ mà chọn
\(\frac{haha}{hihi}\)