Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
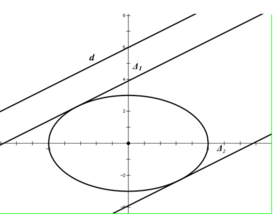
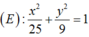có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
Gọi 
là tiếp tuyến của (E) mà 
song song với d
=> x- 2y + C = 0.
Vì d tiếp xúc với (E) nên ta có:
Nên ta có hai tiếp tuyến của (E) song song với d là:
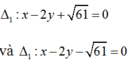
Vậy khoảng cách từ M đến đường thẳng d là lớn nhất là:
, khoảng cách từ M đến đường thẳng d là bé nhất là:
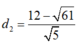
Có: `x-2y+4=0`
`<=>x=2y-4`
Thay `x=2y-4` vào `(E)` có:
`3(2y-4)^2+4y^2-48=0`
`<=>3(4y^2-16y+16)+4y^2-48=0`
`<=>12y^2-48y+48+4y^2-48=0`
`<=>` $\left[\begin{matrix} y=3\\ y=0\end{matrix}\right.$
`@y=3=>x=2.3-4=2`
`@y=0=>x=2.0-4=-4`
`=>` Tọa độ giao điểm của `(E)` và `(d)` là: `(2;3)` và `(-4;0)`
`->D`
\(\Rightarrow\) \(chọn\) \(D\)
\(xét\) \(hpt\) \(:\)
\(\left\{{}\begin{matrix}3x^2+4y^2-48=0\\x-2y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(2y-4\right)^2+4y^2-48=0\\x=2y-4\end{matrix}\right.\)
\(giải:\) \(3\left(4y^2-16y+16\right)+4y^2-48=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}12y^2-48y+48+4y^2-48=0\\16y^2-48y=0\\\left[{}\begin{matrix}y=0\Rightarrow x=-4\\y=3\Rightarrow x=2\end{matrix}\right.\end{matrix}\right.\)
\(vậy\) \(giao\) \(điểm\) \(của\) \(elip\) \(\left(E\right)\) \(là\) \(\left(-4;0\right)\) \(và\) \(\left(2;3\right)\)
Câu 1: Điểm A cho vào để đẹp đội hình hay sao ấy :D
(C) tâm B tiếp xúc với d \(\Rightarrow R=d\left(B;d\right)=\frac{\left|3.3-4\left(-4\right)+5\right|}{\sqrt{3^2+\left(-4\right)^2}}=6\)
Phương trình (C):
\(\left(x-3\right)^2+\left(y+4\right)^2=36\)
Câu 2:
\(c^2=a^2-b^2=5-4=1\Rightarrow F_1F_2=2c=2\)
Độ dài trục lớn:
\(a^2=5\Rightarrow A_1A_2=2a=2\sqrt{5}\)
\(\frac{F_1F_2}{A_1A_2}=\frac{2}{2\sqrt{5}}=\frac{\sqrt{5}}{5}\)
ta có : I = d1 giao d2
=> I(-1,3)
Có (C) tiếp xúc vs dthg d3
=> d(I,d3)=\(\frac{\left|3.\left(-1\right)+4.3-2\right|}{\sqrt{3^2+4^2}}\)=\(\frac{7}{5}\) =R
=> ptr (C): (x+1)2+(y-3)2=\(\frac{49}{25}\)
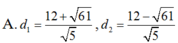
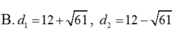
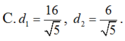
Ta có d: 3x+ 4y -12= 0 ⇔ y = 3 - 3 x 4 , thay vào phương trình E : x 2 16 + y 2 9 = 1 ta được
=> 2 x 2 - 8 x = 0
Vậy d luôn cắt (E) tại hai điểm phân biệt A(0;3) và B(4;0).
Chọn C