Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC

Xét tứ giác CHBK có
\(\widehat{CHB}+\widehat{CKB}=90^0+90^0=180^0\)
=>CHBK là tứ giác nội tiếp
=>C,H,B,K cùng thuộc một đường tròn

có cách này nè:
vẽ nữa (O) kia. vẽ đường kính COK.gọi giao điểm của EM vs CK là F. ta có: tam giác CEK nội tiếp (O), có CK là đường kính => tam giác CEK vuông tại E, có đường cao EF => = CF.CK(1)
ta có: tam giác CMF Đồng dạng với tam giác COH(g.g) => CM/ OC = CF/CH \(\Rightarrow\)CH/CK = CF/CH \(\Rightarrow\)CH2 = CK.CF (2) => từ (1);(2)=> CE=CH. mà ta dễ dàng c/m được CE=CD. vậy CH = CD, nên H thuộc (O;CD). mà CH vuông góc với AB. => dpcm

góc DCA=góc DBA
góc AKB=góc AHB=90 độ
=>AHBK nội tiếp
=>góc AKB+góc AHB=180 độ
=>góc AKH=góc ABH=góc HCD
góc DAC=góc DBC=góc DIH
=>180 độ-góc DAC=180 độ-góc DIH
=>góc CAK=góc HIC
=>góc HAK=góc HIC
mà góc AKH=góc HCI
nên ΔHAK đồng dạng với ΔHIC
=>góc AHK=góc IHC
=>góc IHC+góc KHC=180 độ
=>góc KHI=180 độ
=>K,I,H thẳng hàng

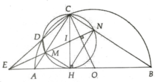
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

a: Xét ΔOBA và ΔOCA có
OB=OC
OA chung
BA=CA
Do đó: ΔOBA=ΔOCA
Suy ra: \(\widehat{OBA}=\widehat{OCA}\)
\(\Leftrightarrow\widehat{OCA}=90^0\)
hay AC\(\perp\)OC tại C
Xét (O) có
OC là bán kính
AC\(\perp\)OC tại C
Do đó: AC là tiếp tuyến của (O)
b: Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2)suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC(3)
Xét (O) có
ΔBCE nội tiếp đường tròn
BE là đường kính
Do đó: ΔBCE vuông tại C
hay BC\(\perp\)CE(4)
Từ (3) và (4) suy ra CE//OA