Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

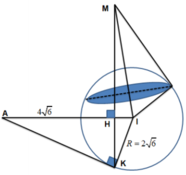
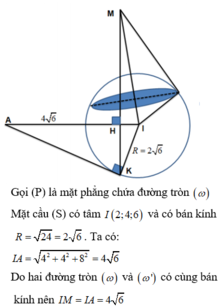
Gọi (P) là mặt phẳng chứa đường tròn ( ω )
Mặt cầu (S) có tâm I(2;4;6) và có bán kính R = 24 = 2 6 . Ta có:
I A = 4 2 + 2 2 + 8 2 = 4 6
Do hai đường tròn ω và ω ' có cùng bán kính nên IA=IM = 4 6
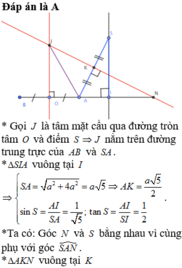
Tam giác IAK vuông tại K nên ta có
I K 2 = I H . I A ⇒ I H = I K 2 I A = 24 4 6 = 6
Do H là tâm của đường tròn ω nên điểm H cố định.
Tam giác IHM vuông tại H nên ta có:
M H = I M 2 - I H 2 = 4 6 2 - 6 2 = 3 10
Do H cố định thuộc mặt phẳng (P), M di động trên mặt phẳng (P) và M H = 3 10 không đổi. Suy ra điểm M thuộc đường tròn có tâm là H và có bán kính r = H M = 3 10
Chọn đáp án B.

Chọn B.
Phương pháp: Coi đáy của hình trụ là mặt phẳng cắt mặt cầu. Áp dụng công thức

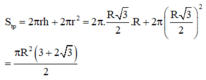

Đáp án B
Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là R 2 = r 2 + h 2 4
Theo bài ra, ta có h = R nên suy ra R 2 = r 2 + h 2 4 ⇔ r 2 = 3 R 2 4 ⇔ r = R 3 2
Diện tích toàn phần hình trụ là:
S t p = 2 πr 2 + 2 πrh = 2 πr r + h = 2 π . R 3 2 . R 3 2 + R = 3 + 2 3 πR 2 2 .

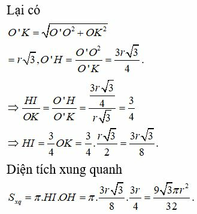
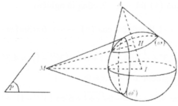


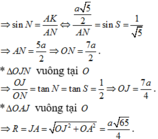

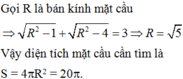
Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P). Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.