Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

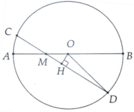
a, Gọi OH là khoảng cách từ O đến CD => MH = 4cm
Tính được OH = 4 3 3 cm
b, Tính được OD = 4 39 3 cm

a: Xét (O) có
\(\widehat{AOM}=\stackrel\frown{AM}\)
\(\widehat{BOM}=\stackrel\frown{BM}\)
mà \(\widehat{AOM}=\widehat{BOM}\)
nên \(\overrightarrow{MA}=\stackrel\frown{MB}\)

Câu a) Hình:
Gọi H và K lần lượt là trung điểm của AB và CD.
=> OH ⊥ AB và OK ⊥ CD ( quan hệ vuông góc giũa đường kính và dây)
Ta có: dây AB = CD (gt)
=> OH = OK ( khoảng cách từ tâm đến dây)
Xét Δ OHM và Δ OKM có:
\(\widehat{OHM}=\widehat{OKM}=90^0\)
OM: chung
OH = OK (cmt)
=> Δ OHM = Δ OKM ( cạnh huyền- cạnh góc vuông)
=> MH = MK (1)
Ta có: HB = HC = \(\frac{1}{2}AB\)
KD = KC = \(\frac{1}{2}CD\)
mà AB = CD (gt)
=> HB = KD (2)
Từ (1) và (2) cộng vế với vế ta được:
MH + HB = MK + KD
⇔ MB + MD ( đpcm)
b) Hình: tự vẽ
Gọi H và K lần lượt là trung điểm của AB và CD
=> OH ⊥ AB và OK ⊥ CD ( quan hệ vuông góc giũa đường kính và dây)
Ta có: dây AB > CD => OH < OK ( khoảng cách từ tâm đến dây)
OH < OK
⇔ OH2 < OK2 ( Chú ý: trong hình học các đoạn thẳng luôn luôn dương nghĩa là độ dài các đoạn thẳng sẽ lớn hơn hoặc bằng 0)
⇔ OH2 + OM2 < OK2 + OM2
Áp dụng dịnh lý Py - Ta - go cho các tam giác vuông OHM vuông tại H, OKM vuông tại K
ta có: MH 2 = OH2 + OM2
MK2 = OK2 + OM2
mà OH2 + OM2 < OK2 + OM2 (cmt)
=> MH2 < MK 2
⇔ MH < MK
*Chúc bạn học tốt*