Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh thuận:
Đường tròn (O) cho trước, điểm A cố định nên OA có độ dài không đổi.
ΔOBC cân tại O (vì OB = OC bán kính)
IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao
OI ⊥ BC
Góc OIA = 90 °
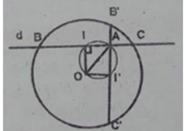
Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định góc góc OIA = 90 ° . Vậy I chuyển động trên đường tròn đường kính OA.
Chứng minh đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’.
Ta chứng minh: I’B = I’C’.
Trong đường tròn đường kính AO ta có góc OI'A = 90 ° (góc nội tiếp chắn nửa đường tròn)
OI'⊥ B'C'
I'B' = I'C' (đường kính vuông góc với dây cung)
Vậy quỹ tích các điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định là đường tròn đường kính AO.
