Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

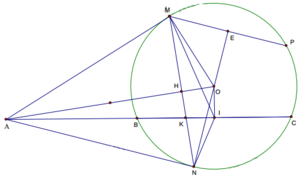
Ta có AN ⊥ NO, MP ⊥ NO, M ∉ AN => AN // MP
Do đó AMPN là hình bình hành ó AN = MP = 2x
Tam giác ∆ANO đồng dạng với ∆NEM => A N N E = N O E M = > N E = 2 x 2 R
TH 1.NE = NO – OE => 2 x 2 R = R − R 2 − x 2 ⇔ 2 x 2 = R 2 − R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 − R t ⇔ 2 t 2 − R t − R 2 = 0 ⇔ 2 t = − R t = R
Do t ≥ 0 ⇒ t = R ⇔ R 2 − x 2 = R ⇔ x = 0 ⇒ A ≡ B (loại)
TH 2 NE = NO + OE => 2 x 2 R = R + R 2 − x 2 ⇔ 2 x 2 = R 2 + R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 + R t ⇔ 2 t 2 + R t − R 2 = 0 ⇔ 2 t = R t = − R
Do t ≥ 0 ⇒ 2 t = R ⇔ 2 R 2 − x 2 = R ⇔ x = R 3 2 = > A O = 2 R (loại)
Vậy A thuộc BC, cách O một đoạn bằng 2R thì AMPN là hbh

O B C A M N I P K J F E
a) Ta thấy \(\widehat{CIP}=\widehat{MIA}\) (Hai góc đối đỉnh)
Các tam giác vuông AMO, AIO và ANO có chung cạnh huyền AO nên A, M, I, O, N cùng thuộc đường tròn đường kính AO.
\(\Rightarrow\widehat{MIA}=\widehat{MNA}\) (Hai góc nội tiếp cùng chắn cung MA)
Mà \(\widehat{MNA}=\widehat{MPN}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
\(\Rightarrow\widehat{CIP}=\widehat{MPN}\)
Chúng lại là hai góc so le trong nên BC // NP.
b) Gọi giao điểm của AO và MN là J, giao điểm của OK với NP là E.
Ta có theo tính chất hai tiếp tuyến cắt nhau thì \(OA\perp MN\)
\(\Rightarrow\Delta AIO\sim\Delta KJO\left(g-g\right)\Rightarrow\frac{AO}{KO}=\frac{OI}{OJ}\Rightarrow OA.OJ=OI.OK\)
Xét tam giác vuông OAM, đường cao MJ, áp dụng hệ thức lượng ta có:
OA.OJ = OM2 = R2
\(\Rightarrow OK.OI=R^2\Rightarrow OK=\frac{R^2}{OI}=const\)
\(S_{ONK}=\frac{1}{2}.OK.NE\le\frac{1}{2}.OK.OF\)
Vậy diện tích tam giác ONK lớn nhất khi NE trùng với OF hay AF vuông góc BC hay BA = R.

a, b, c HS tự làm
d, Gợi ý: G' ÎOI mà I G ' I O = 1 3 => G' thuộc (G'; 1 3 R)

\(S_{OKN}=\dfrac{1}{2}\cdot OK\cdot KN< =\dfrac{1}{2}\cdot\dfrac{OK^2+ON^2}{2}=\dfrac{R^2}{4}\)
Dấu = xảy ra khi MO=MA

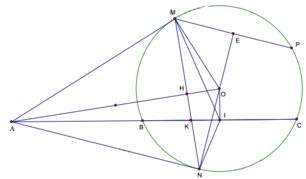
2 A K = 1 A B + 1 A C ⇔ 2 A B . A C = A K ( A B + A C ) ⇔ A B . A C = A K . A I
(Do AB+ AC = 2AI)
∆ABN đồng dạng với ∆ANC => AB.AC = AN2
∆AHK đồng dạng với ∆AIO => AK.AI = AH.AO
Tam giác ∆AMO vuông tại M có đường cao MH => AH.AO = AM2
=> AK.AI = AM2 . Do AN = AM => AB.AC = AK.AI

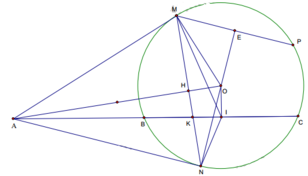
Theo giả thiết AMO = ANO = AIO = 90o = > 5 điểm A, O, M, N, I thuộc đường tròn đường kính AO 0,25
=> AIN = AMN, AIM = ANM (Góc nội tiếp cùng chắn một cung)
AM = AN => ∆AMN cân tại A => AMN = ANM
=> AIN = AIM => đpcm