Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo t/c 2 tiếp tuyến cắt nhau, ta có
góc AOC = góc COM
góc MOD = góc DOB
=> COM +MOD =AOC +BOD = 1/2 AOB = 90o (đpcm)
b) Xét tam giác AOC và tg BDO
Có góc AOC = góc BDO ( cùng phụ BOD)'
góc ACO = góc BOD ( cùng phụ AOC )
=> tg AOC đồng dạng tg BDO (gg)
=> \(\frac{AC}{AO}=\frac{BO}{BD}\Rightarrow AC.BD=AO.BO=R^2\)

c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.

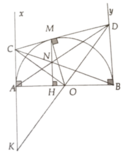
a, Kẻ OM ⊥ CD
Gọi K = OD ∩ d => ∆COK = ∆COD
=> OK = OD => OM = OA = R => CD là tiếp tuyến
b, AC+BD=CM+DM=CD ≥ AB
Do đó min (AC+BD)=AB
<=> CD//AB => ABCD là hình chữ nhật <=> AC = AO
c, AC.BD = MC.MD = O M 2 = 4 a 2
=> 1 O C 2 + 1 O D 2 = 1 4 a 2
d, Từ tính chất hai giao tuyến => MN//BD => MNAB hay MHAB;
AC//BD; MN//BD; NH//BD
=> M N B D = N H B D => MN = NH

a) Xét tứ giác AOMC có
ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối
ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)
hay ˆMAB=ˆOCDMAB^=OCD^
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^
Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù)
mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)
và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)
nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800
⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900
mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)
nên ˆCOD=900COD^=900
Xét ΔCOD có ˆCOD=900COD^=900(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
ˆMAB=ˆOCDMAB^=OCD^(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)
hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)

a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của AM
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
b: CA*BD=CM*MD=OM^2=R^2