Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.

a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: ONMP nội tiếp
=>góc NMO=góc NPO
c: Xét ΔMNA và ΔMBN có
góc MNA=góc MBN
góc NMA chung
=>ΔMNA đồng dạng với ΔMBN
=>MN/MB=MA/MN
=>MN^2=MB*MA

a: góc MNO+góc MPO=90+90=180 độ
=>MNOP nội tiếp
b: MNOP nội tiếp
=>góc NMO=góc NPO

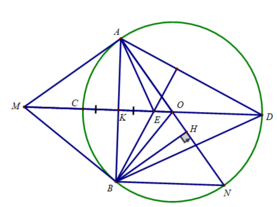
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
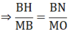
Hay MB. BN = BH. MO

a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)
a: Gọi giao điểm của MN với OA là H
Xét (O) có
AM,AN là tiếp tuyến
Do đó: AM=AN và AO là phân giác của \(\widehat{MAN}\)
AO là phân giác của góc MAN
=>\(\widehat{MAO}=\widehat{NAO}\)
OM=ON
=>O nằm trên đường trung trực của MN(1)
AM=AN
=>A nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra AO là đường trung trực của MN
=>AO vuông góc với MN tại trung điểm của MN
=>AO vuông góc với MN tại H và H là trung điểm của MN
ΔAMO vuông tại M
=>\(MA^2+MO^2=OA^2\)
=>\(MA^2+3^2=5^2\)
=>\(MA^2=5^2-3^2=16\)
=>MA=4(cm)
Chu vi tứ giác OMAN là:
OM+MA+AN+ON
=3+4+4+3
=6+8=14(cm)
Xét ΔOMA vuông tại M có MH là đường cao
nên \(MH\cdot OA=MO\cdot MA\)
=>\(MH\cdot5=3\cdot4=12\)
=>MH=2,4(cm)
H là trung điểm của MN
=>MN=2*MH
=>MN=2*2,4
=>MN=4,8(cm)
b: SO\(\perp\)OM
MA\(\perp\)OM
Do đó: SO//MA
=>\(\widehat{SOA}=\widehat{MAO}\)
mà \(\widehat{MAO}=\widehat{NAO}\)(cmt)
nên \(\widehat{SOA}=\widehat{MAO}=\widehat{NAO}\)
=>\(\widehat{SOA}=\widehat{SAO}\)
=>SA=SO