Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
OA^2=OH*OM
=>OM=9/2=4,5cm
\(HA=\sqrt{3^2-2^2}=\sqrt{5}\left(cm\right)\)
=>\(AB=2\sqrt{5}\left(cm\right)\)
b: Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiếp tuyến của (O)

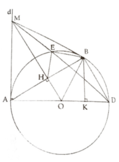
a, Tính được AH = 5 . Từ đó suy ra AB= 2 5 và OM=4,5cm
b, Với ∆MAB cân tại MH là trung tuyến vừa là đường cao;
Ta có ∆MAO = ∆MBO => MBOB => MB là tiếp tuyến của (O)
c, Dễ thấy M A 2 = M H . M O (Theo hệ thức lượng trong tam giác vuông)
Chứng minh được: ∆MBE:∆MBD
=> M B 2 = M E . M D = M A 2
=> MH.MO = ME.MD
=> ∆EHM:∆ODM (c.g.c)
=> E H M ^ = O D M ^
d, Kẻ BK ⊥ AD
Ta có: S H O A = 1 2 S A B D = 1 4 B K . A D
Vì BK ≤ 3 => S H O A lớn nhất khi B là điểm chính giữa cung AD khi đó AM = OA = 3

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')