Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi KC cắt đường tròn (O) lần thứ hai tại I, BK cắt AC tại D. Kẻ đường kính IP của đường tròn (O).
Ta thấy ^IKP chắn nửa đường tròn (O) nên KP vuông góc KI. Mà KN vuông góc KI nên K,N,P thẳng hàng
Dễ dàng chứng minh \(\Delta\)IMO = \(\Delta\)PNO (c.g.c) => ^OIM = ^OPN => IM // PN hay IM // KN
Do KN vuông góc CK nên MI cũng vuông góc CK => ^MIC = ^MAC = 900 => Tứ giác ACIM nội tiếp
Suy ra ^AMC = ^AIC = ^ABK => MC // BK. Khi đó, \(\Delta\)ADB có M là trung điểm AB, MC // BD (C thuộc AD)
=> C là trung điểm AD. Nếu ta gọi BC cắt KH tại S thì \(\frac{HS}{AC}=\frac{KS}{CD}\left(=\frac{BS}{BC}\right)\)(Hệ quả ĐL Thales)
Vậy thì S là trung điểm của KH. Nói cách khác, BC chia đôi KH (tại S) (đpcm).

mình cũng bí câu giống bạn !
Không biết bạn đã có cách giải chưa, chỉ mình với

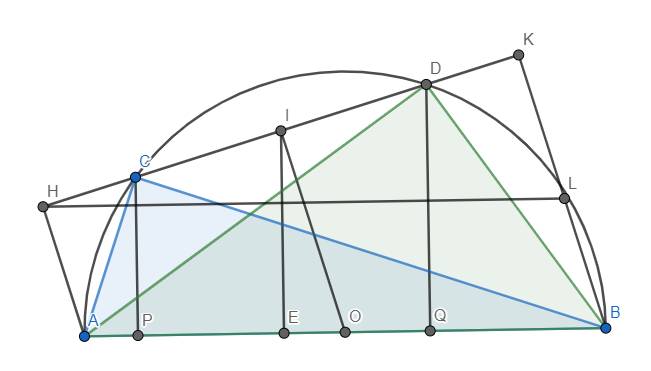
a) Ta thấy OI//AH//BK \(\left(\perp CD\right)\).
Xét hình thang ABKH (AH//BK), O là trung điểm AB. OI//AH \(\left(I\in HK\right)\) nên I là trung điểm HK.
b) Hạ \(CP\perp AB\) tại P, \(DQ\perp AB\) tại Q. Khi đó IE//CP//DQ \(\left(\perp AB\right)\).
Xét hình thang CDQP (CP//DQ) có I là trung điểm CD (hiển nhiên), IE//CP và \(E\in PQ\) nên IE là đường trung bình của hình thang CDQP \(\Rightarrow IE=\dfrac{CP+DQ}{2}\)
Lại có \(S_{ACB}=\dfrac{1}{2}AB.CP\), \(S_{ADB}=\dfrac{1}{2}.AB.DQ\)
\(\Rightarrow S_{ACB}+S_{ADB}=AB.\dfrac{CP+DQ}{2}=AB.IE\) (đpcm)
c) Ta có \(S_{AHKB}=\dfrac{AH+BK}{2}.HK=OI.HK\)
Do dây CD có độ dài không đổi nên khoảng cách từ O đến dây CD là OI cũng không đổi. Như vậy ta chỉ cần tìm vị trí của C để HK lớn nhất.
Thật vậy, dựng hình bình hành ABLH. Khi đó vì BK//AH nên \(L\in BK\). Đồng thời ta luôn có \(HK\le HL=AB\), suy ra \(S_{AHKB}\le OI.AB\).
Dấu "=" xảy ra \(\Leftrightarrow HK=HL\) \(\Leftrightarrow K\equiv L\) \(\Leftrightarrow\) AHKB là hình bình hành \(\Leftrightarrow\) HK//AB hay CD//AB \(\Rightarrow OI\perp AB\). Vậy C là điểm sao cho \(OI\perp AB\).
(Nếu muốn tìm cụ thể vị trí của C, thì mình nói luôn nó là điểm C sao cho \(sđ\stackrel\frown{AC}=180^o-2arc\cos\left(\dfrac{CD}{AB}\right)\) nhé. Chứng minh cái này dễ, mình nhường lại cho bạn.)
Chỗ vị trí C mình sửa lại là \(sđ\stackrel\frown{AC}=90^o-arc\sin\dfrac{CD}{AB}\) nhé.
