Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

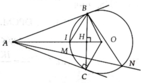
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

a) Nối CE, CF
Xét \(\Delta CEK\) và \(\Delta CFK\) có:
\(\widehat{ECK}\)= \(\widehat{CFK}\) (vì cùng chắn \(\widebat{CE}\))
\(\widehat{CKF}\) chung
\(\Rightarrow\)\(\Delta EKC~\Delta CKF\left(g.g\right)\)
\(\Rightarrow\frac{EK}{CK}=\frac{CK}{FK}\)
\(\Rightarrow CK^2=EK.FK\)(1)
Vì \(\Delta COK\)vuông tại C, \(CM\perp OK\)
\(\Rightarrow CK^2=MK.OK\)(2)
Từ (1), (2) \(\Rightarrow EK.FK=MK.OK\)
\(\Rightarrow\frac{EK}{MK}=\frac{OK}{FK}\)
Xét \(\Delta MEK\)và \(\Delta KOF\)có:
\(\widehat{MKE}\)chung
\(\frac{EK}{MK}=\frac{OK}{FK}\)
\(\Rightarrow\Delta MEK~\Delta FOK\left(c.g.c\right)\)
\(\Rightarrow\widehat{OFE}=\widehat{EMK}\)
\(\Rightarrow\)Tứ giác EMOF nội tiếp

a) Tứ giác MAOB có: \(\widehat{OAM}=90^0\left(0A\perp AM\right);\widehat{OBM}=90^0\left(CB\perp BM\right)\)
=> \(\widehat{OAM}+\widehat{OBM}=180^O\)
=> AOBM nội tiếp (tổng 2 góc đối = 180)
Vì I là tâm=> I là trung điểm OM
b) Tính \(MA^2=3R^2\Rightarrow MC.MD=3R^2\)
c) CM: OM là trung trực AB
=> FA=FB
=> tam giác FAB cân tại F
Gọi H là giao điểm AB và OM
Ta có: OA=OB=AI=R => tam giác OAI đều
=> OAI =60O=> FAB=60o (cùng phụ AFI)
Vậy tam giác AFB đều
d) Kẻ EK vuông góc với FB tại K. Ta có:
\(S_{B\text{EF}}=\frac{1}{2}.FB.EK\)
Mà \(EK\le BE\)( TAM giác BEK vuông tại K)
Lại có: \(BE\le OA\)(LIÊN hệ đường kính và dây cung)
=> \(S_{B\text{EF}}\le\frac{1}{2}.R\sqrt{3}.2R=R^2\sqrt{3}\)
GTLN của \(S_{B\text{EF}}=R^2\sqrt{3}\). kHI ĐÓ BE là đường kính (I)
Kẻ đường kính BG của (I). Vì B và (I) cố định nên BG cố
định . Khi đó vị trí cắt tuyến MCD để \(S_{B\text{EF}}\)đạt GTLN là C là giao điểm của FG với đường tron (O)