Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

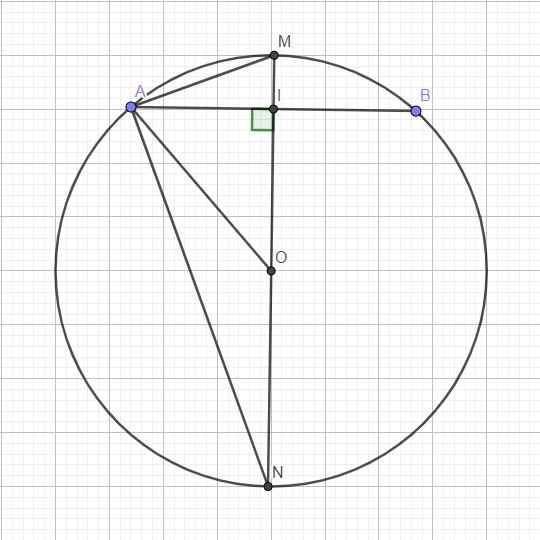
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)

Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.

Bạn tự vẽ hình nha ^-^
a) Xét tứ giác PDKI có PDK=PIK=90
mà 2 góc này ở vị trí đối nhau nên tứ giác PDKI là tứ giác nội tiếp
b)ta thấy : AIQ=1/2 cung AQ
BIQ=1/2 cung QB
mà cung QA=cung QB(gt)
nên IQ là phân giác của AIB
c)
AOQ=45 độ nên sđ cung AQ =45 độ
mà cung AQ= cung QB =45 độ
vậy sđ cung AQB= sđ cung AQ+sđ cung QB=90
d)
Xét tam giác CKI và CPD có
PCD chung
CIK =CDP=90
nên CKI đồng dạng với CPD
vậy \(\frac{CK}{CP}=\frac{CI}{CP}\Leftrightarrow CD\cdot CK=CI\cdot CP\)(CẶP CẠNH TƯƠNG ỨNG)
xét tam giác CAP và CIB có:
PAB chung
APC=CBI(góc nội tiếp cùng chắn cung AI)
nên CAP đồng dạng với CIB
vậy\(\frac{CA}{CI}=\frac{CP}{CB}\Leftrightarrow CA\cdot CB=CI\cdot CP\)
\(\Rightarrow CA\cdot CB=CD\cdot CK\left(=CP\cdot CI\right)\)