Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Theo tính chất 2 tiếp tuyến cắt nhau ta sẽ chứng minh được AM vuông góc với OC, MD vuông góc BD.
Mà \(\widehat{AMB}=90^o\)(góc nội tiếp chắn nửa đường tròn )
Vậy tứ giác OEMF là hình chữ nhật suy ra \(\widehat{COD}=90^O.\)
Trong tam giác vuông OCD, ta áp dụng hệ thức lượng suy ra: \(OM^2=CM.MD\Leftrightarrow R^2=CM.MD\).
Théo tính chât của tiếp tuyến bằng nhau ta có: CM = AC; MD = BD.
Vậy \(AC.BD=R^2.\)
b, Đặt CM = a. R; MD = b.R. Do \(R^2=MC.MD\Rightarrow a.b=1.\)
Áp dụng hệ thức lượng trong tam giác vuông : \(OC^2=CM.CD\Leftrightarrow OC^2=a.R.\left(a.R+b.R\right)\Leftrightarrow OC=R.\sqrt{a\left(a+b\right)}\)
Tương tự \(OD=R.\sqrt{b\left(a+b\right)}.\)
Vậy chu vi tam giác OCD bằng :
\(a.R+b.R+R.\sqrt{a\left(a+b\right)}+R.\sqrt{b\left(a+b\right)}\)
\(=R\left(a+b+\sqrt{a\left(a+b\right)}+\sqrt{b\left(a+b\right)}\right)\)ậy
Suy ra chu vi tam giác OCD min khi : \(a+b+\sqrt{a\left(a+b\right)}+\sqrt{b\left(a+b\right)}\)min.
Có: \(a+b+\sqrt{a\left(a+b\right)}+\sqrt{b\left(a+b\right)}=\sqrt{a+b}\left(\sqrt{a+b}+\sqrt{a}+\sqrt{b}\right)\)
\(=\sqrt{a+b}\left(\sqrt{a+b}+\sqrt{a+b+2}\right)\)
Do a.b = 1 nên a + b min khi a = b = 1 ( áp dụng BĐT cô - si).
Vây MIN \(\sqrt{a+b}\left(\sqrt{a+b}+\sqrt{a+b+2}\right)=\sqrt{2}\left(\sqrt{2}+2\right)=2.\left(\sqrt{2}+1\right)\).
Vậy chu vi tam giác OCD min khi M là trung điểm của CD hay M là trung điểm của cung AB>
\(P_{min}\Delta OCD=2\left(\sqrt{2}+1\right).R\).
qua dễ, lân sau nho hoi nhung bai toan hoc bua ban nhe.

a/ Vì DC, Ax, By là các tiếp của tiếp của đường tròn và cắt nhau tại các điểm tương ứng trên hình vẽ nên ta có
\(\hept{\begin{cases}AC=CM\\BD=MD\end{cases}}\) . Dễ dàng chứng minh góc COD = 90 độ
Áp dụng hệ thức về cạnh trong tam giác vuông , ta có \(MC.MD=OM^2\) hay \(AC.BD=R^2\)
b/ Ta có \(C_{OCD}=OC+OD+CD\) . Để chu vi tam giác OCD nhỏ nhất thì CD nhỏ nhất
Mà CM.MD = R2 không đổi nên CM+MD = CD đạt giá trị nhỏ nhất khi CM = MD
Khi đó M là điểm nằm giữa cung AB trên mặt phẳng chứa C và D.

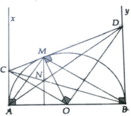
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\cdot180^0=90^0\)
Ta có: MC+MD=CD
nên CD=CA+DB
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(CM\cdot DM=OM^2=R^2\)
hay \(AC\cdot BD=R^2\)

a: Xét (O) có
CM,CA là tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là trung trực của AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: Xét tứ giác MEOF có
góc MEO=góc MFO=góc EOF=90 độ
nên MEOF là hình chữ nhật
=>EF=MO=R

Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân