Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Công thức khoảng cách từ điểm đến đường thẳng
Đặng Ngọc Đăng Thy
Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
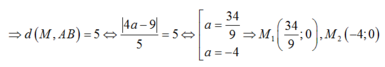
Gọi D là giao điểm MN và BC
Từ M kẻ ME vuông góc BC, từ N kẻ NF vuông góc BC
\(\widehat{B}=\widehat{C}=\widehat{NCF}\Rightarrow\Delta MBE=\Delta NCF\left(ch-gn\right)\)
\(\Rightarrow ME=NF\)
\(\Rightarrow\Delta MED=\Delta NFD\)
\(\Rightarrow MD=ND\) hay D là trung điểm MN
\(\Rightarrow D\left(-1;3\right)\Rightarrow\overrightarrow{ED}=\left(2;4\right)=2\left(1;2\right)\)
Phương trình BC (hay ED) có dạng:
\(2\left(x+3\right)-1\left(y+1\right)=0\Leftrightarrow2x-y+5=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+4=0\\2x-y+5=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;-3\right)\)
\(\Rightarrow\overrightarrow{BM}=\left(3;4\right)\) \(\Rightarrow cosB=\dfrac{\left|3.1+4.2\right|}{\sqrt{3^2+4^2}.\sqrt{1^2+2^2}}=\dfrac{11\sqrt[]{5}}{25}\)
Do C thuộc BC nên tọa độ dạng: \(C\left(c;2c+5\right)\Rightarrow\overrightarrow{NC}=\left(c+1;2c+12\right)\)
\(cosC=cosB=\dfrac{11\sqrt{5}}{25}=\dfrac{\left|1.\left(c+1\right)+2\left(2c+12\right)\right|}{\sqrt{1^2+2^2}.\sqrt{\left(c+1\right)^2+\left(2c+12\right)^2}}\)
\(\Leftrightarrow c^2+10c-96=0\Rightarrow\left[{}\begin{matrix}c=6\Rightarrow C\left(6;17\right)\\c=-16\Rightarrow C\left(-16;-27\right)\end{matrix}\right.\)
(Loại \(C\left(-16;-27\right)\) do D nằm giữa B và C)
Viết phương trình AB (qua M và B), viết phương trình AC (qua N và C). Tọa độ A là giao AB và AC
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0
a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)
Khoảng cách AM là nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của A lên \(\Delta\)
Gọi d là đường thẳng qua A và vuông góc \(\Delta\Rightarrow\) d nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
M là giao điểm của d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+y-2=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)
a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)
Đáp án D
Đường thẳng đi qua 2 điểm A và B có vectơ chỉ phương là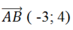
suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
Suy ra phương trình AB: 4( x-3) + 3( y+ 1) = 0 hay 4x+ 3y -9=0
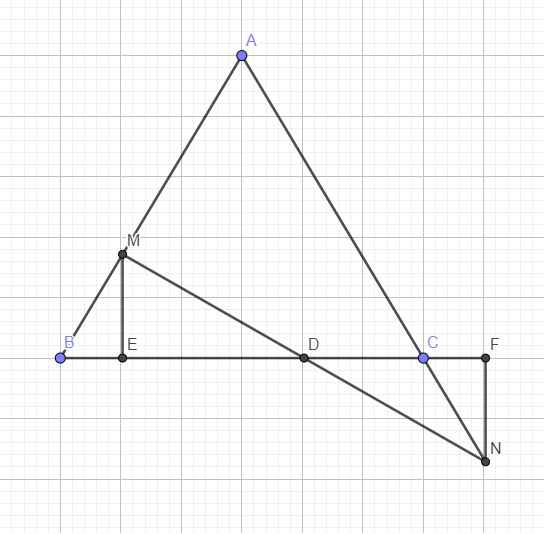
Do M nằm trên Ox nên M( x; 0)
Do d(M; AB)=1 nên