Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D

Để hai đường song song thì m=2 và m-1=1 và m<>-1
=>m=2

Cái này là toán lp 9 mà :D
a/ Để...\(\Leftrightarrow\left\{{}\begin{matrix}m-3\ne1\\2m+1=1\end{matrix}\right.\Leftrightarrow m=0\)
b/ Vì (d1) cắt...
Ta có PTHĐGĐ:
(m-3)x+2m+1=3x-2
Thay x= 2 vào có:
(m-3).2+2m+1= 3.2-2
\(\Leftrightarrow2m-6+2m+1=4\)
\(\Leftrightarrow m=\frac{9}{4}\) (tm)
c/ Vì...
Thay y= -3 vào y= x-5
\(\Rightarrow x=2\)
Thay x= 2; y= -3 vào (d1)
(m-3).2+2m+1= -3
\(\Leftrightarrow2m-6+2m+1=-3\)
\(\Leftrightarrow m=\frac{1}{2}\)



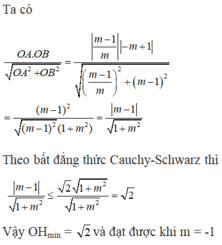

(m-1)x+2m+1=y
=>(m-1)x-y+2m+1=0
\(d\left(O;d1\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+2m+1\right|}{\sqrt{\left(m-1\right)^2+1}}=\dfrac{\left|2m+1\right|}{\sqrt{\left(m-1\right)^2+1}}\)
Để (d) lớn nhất thì \(\sqrt{\left(m-1\right)^2+1}_{Min}\)
=>m=1