Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=ax+b\left(d\right);y=-\dfrac{1}{2}x+\dfrac{1}{2}\left(d'\right)\)
\(\left(d\right)\perp\left(d'\right)\Leftrightarrow-\dfrac{1}{2}a=-1\Leftrightarrow a=2\Rightarrow y=2x+b\left(d\right)\)
Lại có \(\left(d\right)\) đi qua \(A\left(-1;2\right)\Rightarrow2=-2+b\Rightarrow b=4\)
\(\Rightarrow y=2x+4\left(d\right)\)

Đáp án B
Gọi ∆ là đường thẳng cần tìm và n → ( A ; B ) là VTPT của ∆ A 2 + B 2 ≠ 0
Để ∆ tạo với đường thẳng ( d) một góc 450 thì:
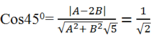
Tương đương: 2( A- 2B) 2= 5( A2+ B2)
Nên A= -3B hoặc B= 3A
+ Với A= - 3B, chọn B= -1 thì A= 3 ta được phương trình ∆ : 3x- y- 5= 0.
+ Với B= 3A, chọn A= 1 thì B= 3 ta được phương trình ∆: x+ 3y- 5 = 0 .

Đáp án D
Gọi ![]()
và A2+ B2> 0 là véc tơ pháp tuyến của
Ta có:
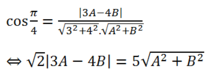
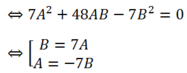
Với B= 7A chọn A= 1 ; B= 7 thì d : x+ 7y+ 5= 0
Với A= -7B chọn A= 7 ; B= 1 thì d : 7x-y-15= 0

bạn xem lại lớp nhé
(d) // đt (delta) <=> \(\left\{{}\begin{matrix}a=5\\b\ne1\end{matrix}\right.\)
=> (d) : y = 5x + b
(d) đi qua M(-1;2) <=> 2 = -5 + b <=> b = 7 (tm)
Vậy (d) : y = 5x + 7

Do A thuộc d1 nên tọa độ có dạng \(A\left(a;3a-3\right)\)
Do B thuộc d2 nên tọa độ có dạng: \(B\left(b;-b-2\right)\)
Áp dụng công thức trung điểm:
\(\Rightarrow\left\{{}\begin{matrix}a+0=2b\\3a-3+2=2\left(-b-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=0\\3a+2b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{3}{4}\\b=-\dfrac{3}{8}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}A\left(-\dfrac{3}{4};-\dfrac{21}{4}\right)\\B\left(-\dfrac{3}{8},-\dfrac{13}{8}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}=\left(\dfrac{3}{8};\dfrac{29}{8}\right)\)
Phương trình d có dạng:
\(29x-3\left(y-2\right)=0\Leftrightarrow29x-3y+6=0\)

a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0
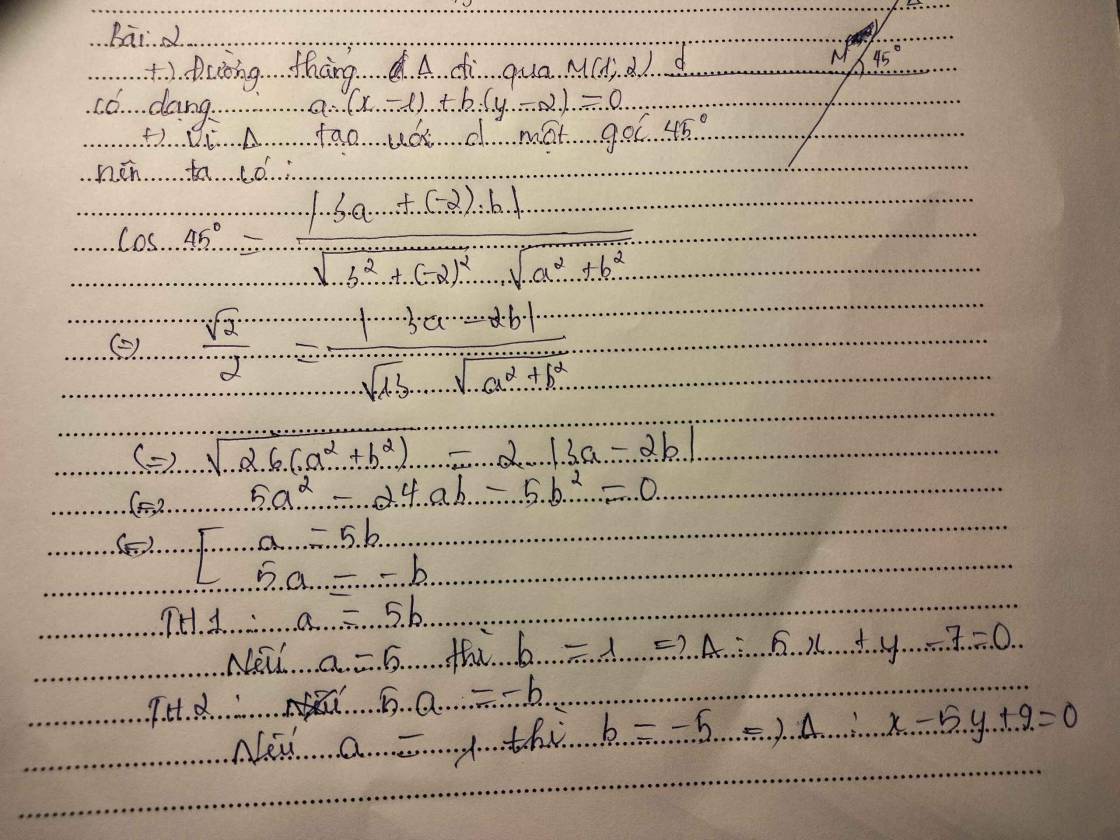

gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M
ôi sai chính tả :< * tối giản