Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Đường tròn (C) có tâm I( 1; -3) và R= 2
![]() có phương trình 4x- 3y+ m= 0.
có phương trình 4x- 3y+ m= 0.
Vẽ
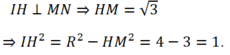
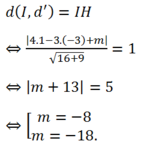

Vậy:
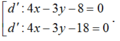

(d')//(d)
=>(d'): 4x-3y+c=0
(C): x^2-4x+4+y^2+6y+9-16=0
=>(x-2)^2+(y+3)^2=16
=>R=4; I(2;-3)
Theo đề, ta có: d(I;(d'))=4
=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
=>|c+17|=4*5=20
=>c=3 hoặc c=-37

Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm \(A\left( {0;4} \right) \in {d_2}\), suy ra \(d\left( {{d_1},{d_2}} \right) = d\left( {A,{d_1}} \right) = \frac{{\left| {4.0 - 3.4 + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\)
Vậy khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\) là 2

M ∈ Δ => M( 1 + 2m ; m)
Do AM // d nên \(\overrightarrow{n_{AM}}=\overrightarrow{n_d}=\left(4;-3\right)\)
Phương trình AM có dạng: 4(x -1 - 2m) - 3(y - m) = 0
Mà A ∈ AM nên: 4(-1 -1 - 2m) - 3(3 - m) = 0
⇔ m= \(\frac{-17}{5}\) => M(\(\frac{-29}{5};\frac{-17}{5}\))

4 câu làm tương tự nhau, nhưng câu a chắc bạn ghi nhầm đề (hoặc đề sai). Do \(AB\perp CC'\) nhưng \(4.2+1.2\ne0\) là hoàn toàn vô lý
Mình làm câu b, 2 câu còn lại bạn làm tương tự
Gọi H là trực tâm tam giác \(\Rightarrow\) H là giao điểm BB' và CC'
Tọa độ H là nghiệm \(\left\{{}\begin{matrix}4x-3y+1=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{64}{29};\frac{95}{29}\right)\)
B là giao điểm BC và BB' nên tọa độ B là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\4x-3y+1=0\end{matrix}\right.\) \(\Rightarrow B\left(-1;-1\right)\)
C là giao điểm BC và CC' nên tọa độ C là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow C\left(2;4\right)\)
Đường AA' đi qua H và vuông góc BC nên nhận \(\left(3;5\right)\) là 1 vtpt
Phương trình AA':
\(3\left(x-\frac{64}{29}\right)+5\left(x-\frac{95}{29}\right)=0\Leftrightarrow3x+5y-23=0\)
Đường thẳng AB qua B và vuông góc CC' nên nhận \(\left(2;-7\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-7\left(y+1\right)=0\Leftrightarrow2x-7y-5=0\)
Đường thẳng AC qua C và vuông góc BB' nên nhận \(\left(3;4\right)\) là 1 vtpt
Phương trình AC:
\(3\left(x-2\right)+4\left(y-4\right)=0\Leftrightarrow3x+4y-22=0\)
Phương trình đường thẳng song song với ∆ có dạng – 4x + 3y + c = 0. Áp dụng công thức khoảng cách giữa hai đường thẳng song song ta có
Đáp án C