Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

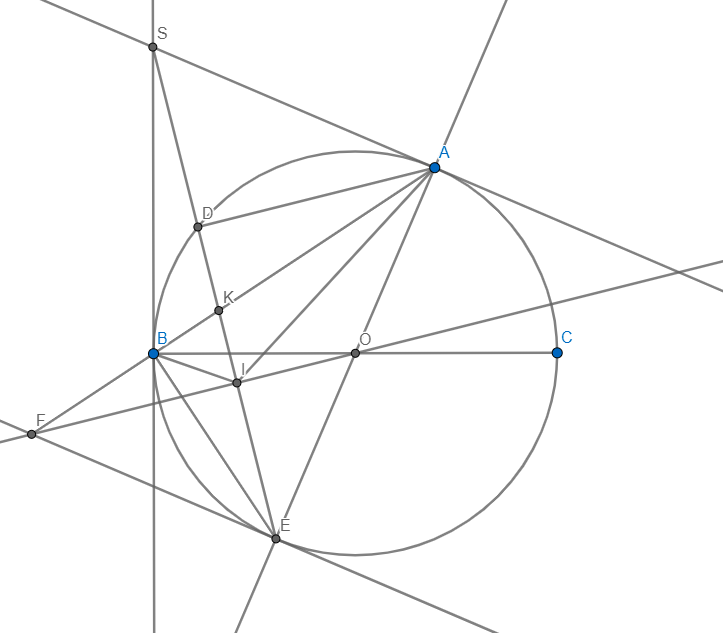
a) Xét tứ giác SAOB có
\(\widehat{SAO}+\widehat{SBO}=180^0\left(90^0+90^0=180^0\right)\)
nên SAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét (O) có
SA là tiếp tuyến có A là tiếp điểm(gt)
SB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: SA=SB(Tính chất hai tiếp tuyến cắt nhau)
Ta có: SA=SB(cmt)
nên S nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OA=OB(=R)
nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra SO là đường trung trực của AB
hay SO\(\perp\)AB(Đpcm)
b) đề phải là \(SA^2=SD.SE\) chứ SD không bằng SE sao \(SD^2=SD.SE\) được
Vì AE là đường kính \(\Rightarrow\angle ADE=90\) mà \(\angle SAE=90\)
\(\Rightarrow\Delta SAE\) vuông tại A có AD là đường cao
\(\Rightarrow SA^2=SD.SE\)
c) Trong (O) có DE là dây cung không đi qua O và I là trung điểm DE
\(\Rightarrow OI\bot DE\Rightarrow\angle OIS=90\Rightarrow\angle OIS=\angle OBS=90\)
\(\Rightarrow OIBS\) nội tiếp mà SAOB nội tiếp (câu a)
\(\Rightarrow O,I,A,S,B\) cùng thuộc 1 đường tròn
\(\Rightarrow AIBS\) nội tiếp \(\Rightarrow\angle AIS=\angle ABS=\angle SAB\) (\(\Delta SAB\) cân tại S)
Xét \(\Delta SAK\) và \(\Delta SIA:\) Ta có: \(\left\{{}\begin{matrix}\angle SIA=\angle SAK\\\angle ISAchung\end{matrix}\right.\)
\(\Rightarrow\Delta SAK\sim\Delta SIA\left(g-g\right)\Rightarrow\dfrac{SA}{SI}=\dfrac{SK}{SA}\Rightarrow SA^2=SK.SI\)
mà \(SA^2=SD.SE\Rightarrow SD.SE=SK.SI\)
d) AB cắt OI tại F'
Vì AE là đường kính \(\Rightarrow\angle ABE=90\Rightarrow F'BE=90\)
\(\Rightarrow\angle F'BE=\angle F'IE\Rightarrow F'BIE\) nội tiếp \(\Rightarrow\angle ABI=\angle F'EI\)
mà \(\angle ABI=\angle ASI\) (AIBS nội tiếp) \(=\angle ASE\)
\(\Rightarrow\angle F'EI+\angle AES=\angle ASE+\angle AES=90\)
\(\Rightarrow\angle F'EO=90\Rightarrow EF'\) là tiếp tuyến \(\Rightarrow\) đpcm

a: Ta có: ΔOBC cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)BC và OK là phân giác của góc BOC
OK là phân giác của góc BOC
=>\(\widehat{BOK}=\widehat{COK}\)
=>\(\widehat{BOD}=\widehat{COD}\)
Xét ΔOBD và ΔOCD có
OB=OC
\(\widehat{BOD}=\widehat{COD}\)
OD chung
Do đó: ΔOBD=ΔOCD
=>DB=DC
ΔOBD=ΔOCD
=>\(\widehat{OBD}=\widehat{OCD}\)
mà \(\widehat{OBD}=90^0\)
nên \(\widehat{OCD}=90^0\)
=>DC\(\perp\)CO tại C
=>DC là tiếp tuyến của (O)
b: Xét tứ giác CHOK có
\(\widehat{CHO}+\widehat{CKO}=90^0+90^0=180^0\)
nên CHOK là tứ giác nội tiếp đường tròn đường kính CO
=>C,H,O,K cùng thuộc một đường tròn
tâm là trung điểm của CO
Bán kính là \(\dfrac{CO}{2}\)

1) Xét tứ giác CIOH có \(\widehat{CIO}+\widehat{CHO}=180^o\)nên là tứ giác nội tiếp
suy ra 4 điểm C,H,O,I cùng thuộc 1 đường tròn
2) vì OI \(\perp\)AC nên OI là đường trung trực của AC
\(\Rightarrow\widehat{AOM}=\widehat{COM}\)
Xét \(\Delta AOM\)và \(\Delta COM\)có :
\(\widehat{AOM}=\widehat{COM}\)( cmt )
OM ( chung )
OA = OC
\(\Rightarrow\Delta AOM=\Delta COM\left(c.g.c\right)\)
\(\Rightarrow\widehat{OAM}=\widehat{OCM}=90^o\)
\(\Rightarrow OC\perp MC\)hay MC là tiếp tuyến của đường tròn O
3) Ta có : \(\hept{\begin{cases}\widehat{AOM}+\widehat{IAO}=90^o\\\widehat{IAO}+\widehat{HBC}=90^o\end{cases}}\Rightarrow\widehat{AOM}=\widehat{HBC}\)
Xét \(\Delta AOM\)và \(\Delta HCB\)có :
\(\widehat{AOM}=\widehat{HBC}\); \(\widehat{MAO}=\widehat{CHB}=90^o\)
\(\Rightarrow\Delta AOM~\Delta HBC\left(g.g\right)\)
4) Gọi N là giao điểm của BC và AM
Xét \(\Delta NAB\)có AO = OB ; OM // BN nên AM = MN
CH // AN \(\Rightarrow\frac{CK}{NM}=\frac{KH}{AM}\left(=\frac{BK}{BM}\right)\)
Mà AM = NM nên CK = KH
\(\Rightarrow\)K là trung điểm của CH

a: Xét (O) có
DA,DC là tiếp tuyến
nên DA=DC và OD là phân giác của góc AOC(1)
mà OA=OC
nen OD là trung trực của AC
Xét (O) có
EC,EB là tiếp tuyến
nên EB=EC và OE là phân giác của góc COB(2)
mà OB=OC
nên OE là trung trực của BC
Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CHOK co
góc CHO=góc CKO=góc HOK=90 độ
nên CHOK là hình chữ nhật
b: OH*OD+OK*OE
=OC^2+OC^2
=2*OC^2