Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔPAN có
PM vừa là đường cao, vừa là trung tuyến
=>ΔPAN cân tại P
b: \(PM=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPAN có
NB,PM là trung tuyến
NB cắt PM tại G
=>G là trọng tâm
GP=2/3*3=2cm
c: CI là trung trực của MP
=>I là trung điểm của MP và CI vuông góc MP tại I
Xét ΔMPN có
I là trung điểm của PM
IC//MN
=>C là trung điểm của PN
=>PM,NB,AC đồng quy

a: \(MN=\sqrt{NP^2-MP^2}=8\left(cm\right)\)
nên NQ=4(cm)
b: Xét ΔQMP và ΔQND có
QM=QN
\(\widehat{MQP}=\widehat{NQD}\)
QP=QD
Do đó; ΔQMP=ΔQND
Suy ra: MP=ND

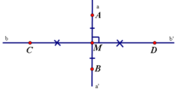
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
+ Trên tia MN có:
MN = 6 cm; MP = 1 cm
Suy ra P nằm giữa M và N (do 6 > 1)
⇒ MP + PN = MN ⇒ PN = MN – MP = 6 – 1 = 5 cm
+ Trên tia NM có:
NM = 6 cm; NQ = 1 cm
Suy ra Q nằm giữa M và N (do 6 > 1)
⇒ NQ + QM = NM ⇒ QM = NM – NQ = 6 – 1 = 5 cm
Do đó: PN = QM (= 5 cm) A đúng
+ Gọi A là trung điểm của đoạn thẳng MN ⇒ AM = AN = 1/2 MN = 3 cm
Gọi d là đường thẳng đi qua A và vuông góc với MN tại A
Do đó d là đường trung trực của đoạn thẳng MN
Vì P và Q đều thuộc MN, nên suy ra d ⊥ PQ (1) ⇒ B đúng
+ Trên tia MN có MA = 3 cm; MP = 1 cm
Suy ra P nằm giữa M và A ⇒ MP + PA = MA ⇒ PA = MA – MP = 3 – 1 = 2 cm
Chứng minh tương tự ta có: NQ + QA = NA ⇒ QA = NA – NQ = 3 – 1 = 2 cm
Do đó: PA = QA, mà P, Q, A thẳng hàng (do P, Q, A đều thuộc MN)
Suy ra A là trung điểm của PQ (2)
Từ (1) và (2) suy ra d là đường trung trực của đoạn thẳng PQ ⇒ C đúng
Chọn đáp án D