Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

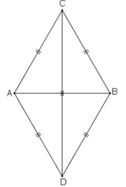
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

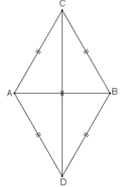
Xét ΔACD và ΔBCD, ta có:
AC = BC (= AB)
CD cạnh chung
AD = BD (= AB)
Suy ra: ΔACD = ΔBCD(c.c.c)

Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải


a) Xét tam giác NMA và NMB có:
\(MA=MB\left(gt\right)\)
\(NM\) là cạnh chung.
\(NA=NB\) (đường tròn tâm A và B cùng bán kính cắt nhau)
\(\Rightarrow\Delta NMA=\Delta NMB\left(c.c.c\right)\) (1)
b) Vì \(\widehat{NMA}=\widehat{NMB}\) (từ 1) và 2 góc trên là 2 góc kề bù nên \(\widehat{NMA}=\widehat{NMB}=90^o\)
Vậy \(NM\perp AB\)
c) \(NA=NB\) (từ 1)
\(BM=\dfrac{AB}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Chu vi tam giác NMB:
\(10+8+6=24\left(cm\right)\)

a: Xét ΔABC và ΔABD có
AB chung
BC=BD
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔACD và ΔBCD có
AC=BC
CD chung
AD=BD
Do đó:ΔACD=ΔBCD

a: xét tam giác abc và tam giác abd có
- ab chung
- ac=ad
- cd=bd
suy ra tam gics abc= tam giác abd (c-c-c)
b:xét tam giác acd và tam giác bcd có
-cd chung
- ac=ad
- cb=bd
suy ra tam giác acd= tam giác bcd (c-c-c)

Hướng dẫn:
Có: BM = BN ( = BA ) => B thuộc đường trung trực của MN (1)
Có: AM= AN (= AB ) => A thuộc đường trung trực của MN (2)
Từ (1) , (2) => AB là đường trung trực MN => AB vuông góc MN.
Vì M, N thuộc (B; AB)
=>MB=NB(1)
Vì M, N thuộc (A; AB)
=>MA=MB(2)
Từ (1) và (2)
=>B, A nằm trên trung trực của MN(3)
=>AB vuông với MN(vì AB là tt MN có được từ điều 3)