
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1( Hình mik đăng lên trước nha, mới lại phần bn nối điểm K với B, điểm F với D hộ mik nhé)
a) Xét tam giác EFA và tam giác CAB, có:
AE = AC ( giả thiết)
AF = AB (giả thiết)
Góc EAF = góc BAC (2 góc đối đỉnh)
=> ΔEAF = ΔCAB (c.g.c)
b) Vì ΔEFA = ΔCAB (Theo a)
=> Góc ABC = Góc EFA (cặp góc tương ứng)
=> EF = BC (cặp cạnh tương ứng) (1)
Mà EK = KF = 1/2 EF (2)
BD = DC = 1/2 BC (3)
Từ (1), (2) và (3)
=> KF = BD
Xét ΔKFB và ΔFBD, có
Cạnh BF chung
KF = BD (chứng minh trên)
Góc EFB = Góc ABC (chứng minh trên)
=> ΔKFB =ΔDBF (c.g.c)
=> KB = FD (cặp cạnh tương ứng)

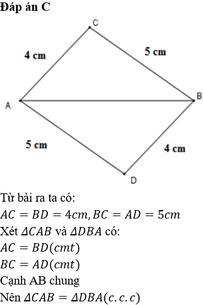
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

Giải:
a) Xét \(\Delta BAC,\Delta ECA\) có:
\(AB=CE\left(gt\right)\)
\(\widehat{BAC}=\widehat{ECA}\left(=90^o\right)\)
\(AC\): cạnh chung
\(\Rightarrow\Delta BAC=\Delta ECA\left(c-g-c\right)\)
\(\Rightarrow BC=AE\) ( cạnh t/ứng ) ( đpcm )
\(\Rightarrow\widehat{BCA}=\widehat{EAC}\) ( góc t/ứng )
Mà 2 góc trên ở vị trí so le trong nên BC // AE ( đpcm )
b) Ta có: \(\widehat{EAC}+\widehat{ECA}=\widehat{AEx}\) ( góc ngoài \(\Delta ECA\) )
\(\Rightarrow\widehat{EAC}+90^o=120^o\)
\(\Rightarrow\widehat{EAC}=30^o\)
Mà \(\widehat{BCA}=\widehat{EAC}\Rightarrow\widehat{BCA}=30^o\)
Xét \(\Delta ABC\) có: \(\widehat{BCA}+\widehat{ABC}=90^o\) ( do \(\widehat{A}=90^o\) )
\(\Rightarrow\widehat{ABC}=60^o\) ( do \(\widehat{BCA}=30^o\) )
Vậy...

a: Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
Do đó: ΔABI=ΔACI
b: Xét tứ giác ABDC có
I là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD
c:
Ta có: AI\(\perp\)BC
BE\(\perp\)BC
Do đó: AI//BE
Xét tứ giác ABEI có
AI//BE
AI=BE
Do đó: ABEI là hình bình hành
=>AE cắt BI tại trung điểm của mỗi đường
mà O là trung điểm của BI
nên O là trung điểm của AE
=>A,O,E thẳng hàng