Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA ,và MB.

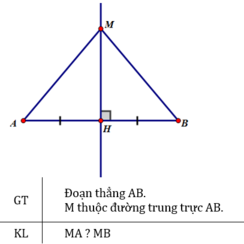
Gọi H là giao điểm của đường trung trực với đoạn AB
⇒ H là trung điểm AB và MH ⊥ AB.
Xét ΔAHM và ΔBHM có:

Nên ΔAHM = ΔBHM
Vậy MA = MB



Đặt AB vương góc với đường trung trực tại E
xét 2 TG AME và BME, ta có
AE=BE (gt) AEM=BEM=90 độ ME cạnh chung
suy ra TG AME=TG BME (cgc)
suy ra MA=MB

Gọi NM là trung trực AB
=> NA = NB và góc MNA = góc MNB = 90o (Tính chất đường trung trực)
Xét tam giác MNA và tam giác MNB có:
góc MNA = góc MNB (= 90o)
Chung NM
NA = NB (cmt)
=> tam giác MNA = tam giác MNB (c.g.c)
=> MA = MB (2 cạnh tương ứng)

H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!

xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)
Hình vẽ: tự vẽ
Đặt AB vuông góc với đường trung trực tại E.
Xét 2 TG AME và BME, ta có:
AE=BE(gt); AEM=BEM=90o; ME; cạnh chung.
=>TG AME=TG BME(c.g.c)
=>MA=MB(2 cạnh tương ứng).