
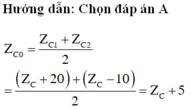
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

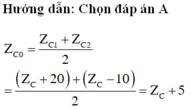

Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$

\(P_1 = P_2 <=> I_1^2R = I_2^2 R\)
<=> \(\frac{U^2}{Z_1^2} R = \frac{U^2}{Z_2^2}R\)
<=> \(Z_1^2 = Z_2^2\)
<=> \(R^2 +(Z_L-Z_{C1})^2 = R^2 +(Z_L-Z_{C2})^2\)
<=> \((Z_L-Z_{C1})^2 =(Z_L-Z_{C2})^2 \)
Mà \(Z_{C1} \neq Z_{C2}\) => \(Z_L - Z_{C1} = -(Z_L-Z_{C2})\)
=> \(Z_L = \frac{Z_{C1}+Z_{C2}}{2} \)
mà công suất của mạch cực đại khi \(Z_L = Z_C => Z_C = \frac{Z_{C_1}+Z_{C_2}}{2}\)
=> \(\frac{1}{C\omega} = \frac{1}{2}(\frac{1}{C_1\omega}+\frac{1}{C_2\omega} )\)
=> \(\frac{1}{C} = \frac{1}{2}(\frac{1}{C_1}+\frac{1}{C_2} ) = \frac{1}{2} (\frac{\pi}{2.10^{-4}}+\frac{3\pi}{2.10^{-4}})\)
=> \(C = \frac{10^{-4}}{\pi} F.\)

Từ đồ thị ta có: P Y max = 3 2 P X max ⇒ R X = 3 2 R Y
Mặc khác:
P X max = 2 P X ω 2 ⇔ U 2 R X = U 2 R X R X 2 + L 1 ω 2 − 1 C 1 ω 2 ⇒ L 1 ω 2 − 1 C 1 ω 2 = ± R 1
Ta chọn nghiệm L 1 ω 2 − 1 C 1 ω 2 = R X vì đồ thị P X tại giá trị ω 2 mạch đang có tính cảm kháng
Ta chọn nghiệm L 2 ω 2 − 1 C 2 ω 2 = − R Y vì đồ thị P Y tại giá trị ω 2 mạch đang có tính dung kháng
Công suất tiêu thụ của đoạn mạch AB tại ω 2 :
P = U 2 R 1 + R 2 R 1 + R 2 2 + L 1 + L 2 ω 2 − 1 C 1 + 1 C 2 1 ω 2 = U 2 R 2 1 + 3 2 1 + 3 2 2 + 3 2 − 2 2
Từ đó ta tính được P ω 2 = 23 , 97 W
Đáp án B